Příklad 2.8
Jaká je pravděpodobnost, že rodina se třemi dětmi má dva chlapce a jedno děvče za podmínky, že má alespoň jednoho chlapce?
Řešení:
Jev A - dva chlapci a jedno děvče.
Jev B - alespoň jeden chlapec.
![]()
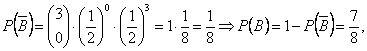
![]()

Příklad 2.9
Sodovkárna má dva automaty na plnění a uzavírání lahví. První automat zpracuje 1000 lahví za hodinu, druhý automat zpracuje 1500 lahví za hodinu. Z tohoto počtu má zpravidla pět lahví z prvního a dvanáct lahví z druhého automatu vadný uzávěr.
Máme za úkol určit:
1) Má-li láhev vadný uzávěr, jaká je pravděpodobnost, že pochází z druhého automatu?
2) Jaká je pravděpodobnost, že náhodně vybraná láhev je vadná?
Řešení:
Jev A značí, že láhev má vadný uzávěr.
![]()
![]()
Pravděpodobnost, že láhev je vadná a je z prvního automatu:
![]()
Pravděpodobnost, že láhev je vadná a je z druhého automatu:
![]()
ad 1) Má-li láhev vadný uzávěr, pochází z druhého automatu s pravděpodobností:
![]()
S pravděpodobností 70,6 % bude vadná láhev pocházet z druhého automatu.
ad 2) Pravděpodobnost, že náhodně vybraná láhev je vadná:
![]() .
.
Vadná láhev je vybrána s pravděpodobností 0,68 %.
Příklad 2.10
Hodíme dvěma kostkami, bílou a černou. Jaká je pravděpodobnost, že na bílé padlo číslo menší než 4 za podmínky že padl součet 7.
Řešení:
Jev A – součet je 7.
Jev B – číslo menší než 4 na bílé kostce.
![]()
(Podobně jako v příkladu 2.1 b),
![]()
![]()
(průnik jevů je jejich součin),

Na bílé kostce padne číslo menší než 4 s celkovým součtem 7 s pravděpodobností 50 %.