Příklad 2.1

Hodíme bílou a černou kostkou, b značí číslo na bílé kostce, c číslo na černé kostce. V každém z následujících případů rozhodněte, zda jevy jsou nebo nejsou závislé.

a) Jev A je b = 3, jev B je c = 4.

Řešení:

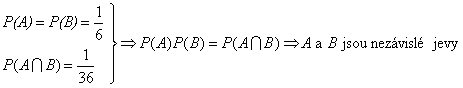
b) Jev C je b + c = 7, jev D je c = 3.

Řešení:

c) Jev C je b + c = 7, jev E je c < 3.

Řešení:

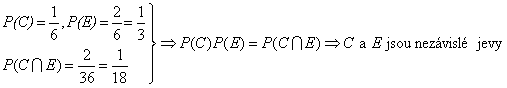
d) Jev F je b + c = 11, jev G je c ≠ 5.

Řešení:

Jevy v bodech a), b) a c) nejsou na sobě nezávislé a v bodě d) jsou jevy na sobě závislé.

Příklad 2.2

Čtyři stroje pracují nezávisle na sobě a mají různou poruchovost. Pravděpodobnost, že během jedné hodiny dojde k poruše na prvním stroji je P(A₁) = 0,1; na druhém stroji P(A₂) = 0,2; na třetím stroji P(A₃) = 0,3; na čtvrtém stroji P(A₄) = 0,05. Jaká je pravděpodobnost, že během jedné hodiny nedojde k žádné poruše?

Řešení:

Pravděpodobnost, že během jedné hodiny nedojde k žádné poruše, je 47,9 %.

Příklad 2.3

Pracovník má navštívit tři arabská města postižená nemocí. Pravděpodobnost nakažení v některém městě je: P(A) = 0,3; P(B) = 0,4; P(C) = 0,5. Jaká je pravděpodobnost, že se v některém z těchto měst nakazí?

Řešení:

Pravděpodobnost, že se pracovník během své cesty nakazí, je 79 %.

Příklad 2.4

S jakou pravděpodobností bude sdružená telefonní linka s 10 účastníky obsazena, je-li pro každého účastníka pravděpodobnost hovoru v daném okamžiku 1 % a vyskytují-li se hovory nezávisle na sobě?

Řešení:

Linka bude v daném okamžiku obsazena s pravděpodobností 9,5 %.