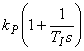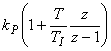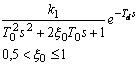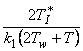3.4. Metoda požadovaného modelu (inverze dynamiky)

Metoda umožňuje snadné a rychlé seřízení standardních typů číslicových a analogových regulátorů pro základní druhy regulovaných soustav s dopravním zpožděním. Typ regulátoru je doporučen z hlediska vlastností regulované soustavy a požadavku na nulovou trvalou regulační odchylku způsobenou skokovou změnou polohy žádané veličiny, resp. poruchy působící na výstupu regulované soustavy, viz obr. 23.

Obr. 23. Regulační obvod

regulátory

Předpokládá se použití standardních analogových a číslicových regulátorů s odpovídajícími L- a Z-přenosy v souladu s tab. 8.

Tab. 8. Přenosy standardních regulátorů

Typ	Analogový regulátor	Číslicový regulátor
P
I
PI
PD
PID

U číslicových regulátorů není uvažováno kvantování, integrace je realizována zpětnou (levou) obdélníkovou sumací a derivace zpětnou diferencí.

Regulované soustavy

Aby bylo možné metodu požadovaného modelu (inverze dynamiky) použít, musí být přenos regulované soustavy   v jednom ze základních tvarů uvedených v tab. 10.

Pro aperiodické regulované soustavy bude ukázáno získání náhradních přenosů v základních tvarech (27) a (28) z přechodové charakteristiky, případně transformací z tvaru (32).

Předpokládá se, že aperiodická regulovaná soustava může být aproximována jedním z náhradních přenosů

                                                                                                          (27)

resp.

                                                                                                  (28)

Dopravní zpoždění  T_d1, resp. T_d2 u regulované soustavy může být přirozené nebo může vzniknout aproximací setrvačnosti vyššího řádu. Koeficient přenosu  k₁  je u proporcionálních regulovaných soustav dán ustáleným stavem na přechodové charakteristice, tj.

 .                                                                                                                      (29a)

Pokud vstupní skok není jednotkový, pak je dán poměrem změny výstupní veličiny  y  ke změně vstupní veličiny u  v ustáleném stavu, tj.

 .                                                                                                                          (29b)

Hodnoty dalších parametrů  T₁ a T_d1, resp. T₂  a  T_d2  je možno snadno určit experimentálně z přechodové charakteristiky regulované soustavy  h_S(t) na základě vztahů (obr. 24) :

,                                                          (30)

resp.

.                                                           (31)

Obr. 24. Přechodová charakteristika regulované soustavy

Pro identifikaci aperiodických regulovaných soustav vyššího řádu se často používá náhradní přenos

.                                                                                                  (32)

Rychlé převedení přenosu (32) na požadované tvary (27) a (28) umožňuje tab. 9, kterou je možno rovněž využít pro převody v souladu se schématem (33)

                                                     

                                                                                                                                   (33)

                                              

Pro získání přenosu v některém ze zbývajících tvarů je nutno použít vhodných identifikačních či aproximačních metod.

Tab. 9. Převedení přenosu regulované soustavy na požadované tvary

	n	1	2	3	4	5	6
		1	1,568	1,980	2,320	2,615	2,881
		0	0,552	1,232	1,969	2,741	3,537
		0,638	1	1,263	1,480	1,668	1,838
		-0,352	0	0,535	1,153	1,821	2,523

T_d1  0,352T₁

Seřízení regulátorů

Na základě metody požadovaného modelu (inverze dynamiky) a následného simulačního upřesnění byly získány tab. 10 a 11, které umožňují jednoduché a rychlé určení hodnot stavitelných parametrů doporučovaných regulátorů (Vítečková, 1998).

Pro regulované soustavy bez dopravního zpoždění (T_d = 0) se předpokládá požadovaný průběh přechodové charakteristiky  h_w(t) uzavřeného regulačního obvodu podle obr. 25a. Časová konstanta T_w   musí být zvolena s ohledem na omezení akční veličiny a maximální nastavitelnou hodnotu zesílení regulátoru  k_Pmax  a u regulačního obvodu s číslicovým regulátorem musí navíc platit

 .                                                                                                                        

a)                                                                      b)

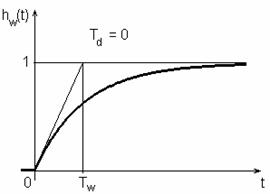
Obr. 25. Požadovaná přechodová charakteristika uzavřeného regulačního obvodu:
 a) bez dopravního zpoždění, b) s dopravním zpožděním

Pro regulované soustavy s dopravním zpožděním (T_d 0) na základě požadovaného relativního překmitu  (0 0,5) u přechodové charakteristiky h_w(t) uzavřeného regulačního obvodu (viz obr. 25b), tab. 11 a vztahu

                                                                                                                     (34)

se určí pro doporučený typ regulátoru z tab. 10 odpovídající hodnoty jeho stavitelných parametrů. Pokud dopravní zpoždění  T_d    je velmi malé, hodnotu určeného koeficientu  a  je třeba vhodně snížit s ohledem na omezení akční veličiny a maximální nastavitelnou hodnotu zesílení regulátoru  k_Pmax .

Tab. 10 a vztah (34) pro  T 0 platí pro číslicové regulátory a pro  T = 0  pro analogové regulátory.

Přesnost seřízení je okolo 5% u číslicových regulátorů a u analogových regulátorů je podstatně lepší. Požadovaný průběh  je možno „doladit“ vhodnou úpravou zesílení regulátoru  k_P.

Při volbě vzorkovací periody  T  u číslicových regulátorů je třeba splnit podmínky (Isermanm, 1981; Vítečková, 1998)

kde  t_0,95  je doba, za kterou přechodová charakteristika regulované soustavy  h_S(t) dosáhne 95% své ustálené hodnoty, T_d - dopravní zpoždění regulované soustavy, např. vyplývající z náhradního přenosu (27), resp. (28).

Vztahy pro určení hodnot stavitelných parametrů číslicových regulátorů v tab. 10 jsou pouze přibližné. Přesné vztahy jsou uvedené např. v (Vítečková, 1998).

 

Tab. 10. Doporučené typy regulátorů a výpočet jejich stavitelných parametrů

regulovaná soustava	regulátor
	TYP
		Td = 0	Td0
	P			-	-
	PI				-
	PD			-
	PID
	PID

Tab. 11. Hodnoty koeficientů a

κ	0	0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,45	0,50
a	1,282	0,984	0,884	0,832	0,763	0,697	0,669	0,640	0,618	0,599	0,577
β	2,718	1,944	1,720	1,561	1,437	1,337	1,248	1,172	1,104	1,045	0,992

 

příklad použití

Pro regulovanou soustavu s dopravním zpožděním

je třeba navrhnout číslicový a analogový regulátor typu PI a PID. Regulátory je třeba seřídit tak, aby byl zajištěn relativní překmit přechodové charakteristiky regulačního obvodu = 0,05 (5%) pro T = 2.

Řešení:

Nejdříve se určí náhradní přenosy ve tvaru (27) a (28) v souladu se schématem (33) při použití tab. 9. Pak pro tyto náhradní přenosy pomocí tab. 10 a 11 se určí typ regulátoru a vypočítají se hodnoty jeho stavitelných parametrů.

Ze zadání přenosu regulované soustavy vyplývá: n = 3,  k₁ = 2,  T₃ = 4  a  T_d3 = 10.

a) PI regulátor

Pro přenos    z tab. 9 se dostane:

;     

Číslicový PI regulátor

Pro překmit = 0,05  a  k₁ = 2, T₁ = 7,92, T_d = T_d1 = 14,928,  T = 2 z tab. 11 a 10 se dostane:

       

             

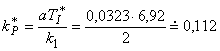
Analogový PI regulátor (T = 0)

                                                

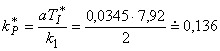
b) PID regulátor

Pro přenos 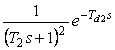 z tab. 9 se dostane:

;  

Číslicový PID regulátor

Pro překmit = 0,05  a  k₁ = 2, T₁ = T₂ = 5,052,  T_d = T_d2 = 12,14,  T = 2 z tab. 11 a 10 se dostane:

             

;

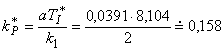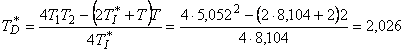
Analogový PID regulátor (T = 0)

                   

                    

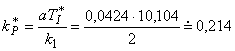
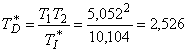
Přechodové charakteristiky regulované soustavy a jejích náhradních přenosů jsou na obr. 26a. Na obr. 26b jsou přechodové charakteristiky uzavřeného regulačního obvodu. Všechny průběhy byly získány číslicovou simulací pomocí simulačního programu SIPRO (Farana, 1996).

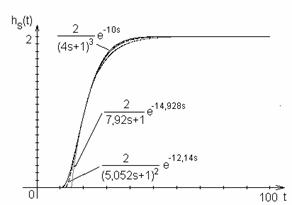
Obr. 26a. Přechodové charakteristiky regulované     Obr. 26b. Přechodové charakteristiky
soustavy a její aproximace                                          uzavřeného regulačního obvodu

 

Uvedený přístup umožňuje jednoduché seřízení standardních typů číslicových
a analogových regulátorů pro regulované soustavy s dopravním zpožděním. Pokud dosažená kvalita regulace je nedostačující, je nutno použít nestandardní typ regulátoru [např. Smithův, resp. modifikovaný Smithův regulátor (Isermann, 1981)], případně složitější strukturu regulačního obvodu (Åström, K. – Hägglund, 1995; Isermann, 1981)