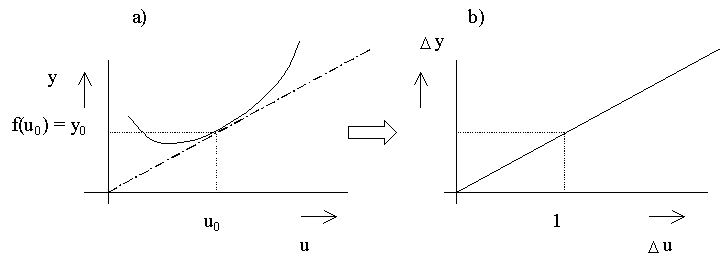

Z důvodů co nejlepšího zachování vlastností systému linearizujeme charakteristiky pouze v pracovním bodě (pokud se pracovní bod posune - je třeba provést linearizaci znovu).
Pracovní bod : u0, y0
Linearizace tečnou
Uvažujeme dynamický systém (DS) s více vstupy
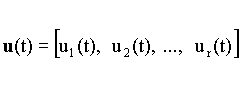 .
.
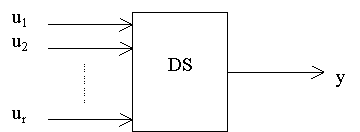
Obr. 5 Linearizace tečnou
Předpokládáme nelineární statickou charakteristiku : y(t) = f(u)
V okolí zvoleného nebo zadaného pracovního bodu u nelineární funkci f(u) rozvineme v Taylorovu řadu [Víteček, A. a Wawrziczková, M. 1986]
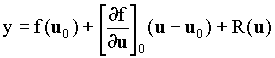
kde R(u) je zbytek Taylorova rozvoje, který zanedbáváme.
Po zanedbání zbytku R(u) dostaneme linearizovanou rovnici
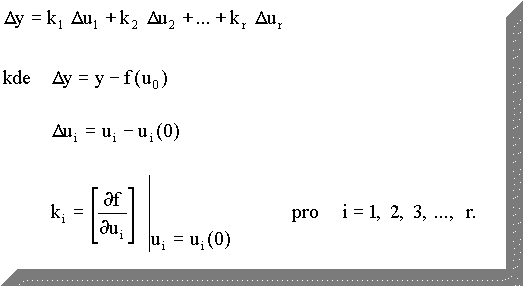
Vz. 57
Velmi důležité je, že po provedené linearizaci musíme nový počátek souřadnicového systému přesunout do pracovního bodu (u0, y0). Tzn. s linearizovaným modelem musíme pracovat v přírůstkových souřadnicích (obr. 4b), jinak by nebyla splněna podmínka linearity. Z obr. 4a vyplývá, že linearizovaný model bude platit pouze pro malé změny vstupního signálu v okolí pracovního bodu.
Linearizace z naměřených hodnot
N naměřených hodnot :
![]()
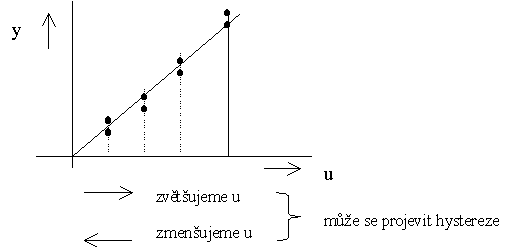
Obr. 6 Linearizace z naměřených hodnot
Pro aproximaci použijeme metodu nejmenších čtverců :

Výsledný vztah pro určení směrnice přímky linearizovaného matematického modelu dynamického systému je :
![]()
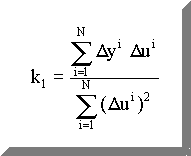
Vz. 58
Uvedené metody jsou v praxi používány často, hlavně pro svou jednoduchost. Metody linearizace nelze aplikovat na tzv. podstatně nelineární systémy, u kterých by se linearizací statické vlastnosti změnily zásadním způsobem.