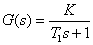
Aproximace proporcionální soustavou se setrvačností 1.řádu
Aproximace přechodové charakteristiky s kmitavým průběhem
Aproximace přechodových charakteristik s aperiodickým průběhem - Strejcova metoda
Vyhodnocení přechodové charakteristiky integrační soustavy
Vyhodnocení integrační soustavy se setrvačností
Aproximace odezev derivačních členů
Soustavy s dopravním zpožděním
Aproximace pomocí tečny v inflexním bodě
Aproximace pomocí sečny v inflexním bodě
Aproximace pomocí tečny a sečny v inflexním bodě
Aproximace dvoubodovou metodou - varianta č. 1
kde K - zesílení soustavy, T1 - časová konstanta.
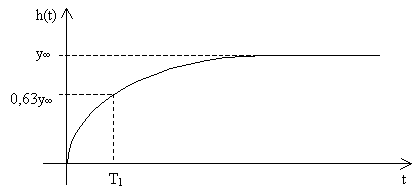
Obr. 1 Aproximace přechodové charakteristiky proporcionální soustavy se setrvačností 1.řádu
Nejdříve zjistíme ustálenou hodnotu výstupní a vstupní veličiny. Jejich podílem získáme zesílení K.
kde u(¥) - ustálená hodnota vstupní veličiny, y(¥) - ustálená hodnota výstupní veličiny. Časovou konstantu T1 určíme z hodnoty 0,63y(¥)
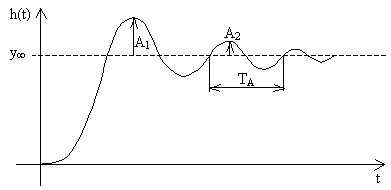
Obr. 2 Aproximace přechodové charakteristiky s kmitavým průběhem
Přechodová charakteristika s kmitavým průběhem je popsána přenosem:
Parametry tohoto přenosu stanovíme následujícím postupem:
kde υ - logaritmický dekrement útlumu, ξ - součinitel poměrného tlumení, T0 - časová konstanta.
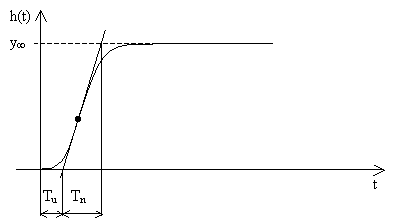
Obr. 3 Přechodová charakteristika s aperiodickým průběhem a s vyznačenou dobou náběhu a dobou průtahu
Vykazuje-li odezva systému aperiodický průběh, lze ji aproximovat pomocí proporcionální soustavy 2.řádu s rozdílnými časovými konstantami nebo proporcionální soustavou n-tého řádu se stejnými časovými konstantami. Volba soustavy záleží na hodnotě parametru τ, který se vypočte:
kde Tu - doba průtahu, Tn - doba náběhu.
Pokud parametr τ je menší než 0,1, volíme pro aproximaci obrazový přenos s rozdílnými časovými konstantami. Pokud je τ větší než 0,1, volíme obrazový přenos se stejnými časovými konstantami. Tedy:
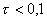 | => aproximujeme přenosem ve tvaru: |  |
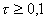 | => aproximujeme přenosem ve tvaru: | 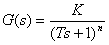 |
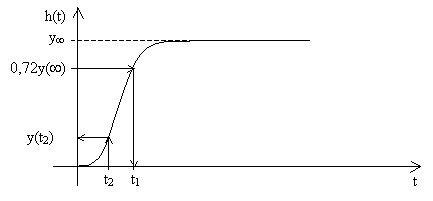
Obr. 4 Aproximace proporcionální soustavou 2.řádu s rozdílnými časovými konstantami
| Parametry přenosu |  |
určíme následujícím postupem: |
- Pro hodnotu 0,72y(¥) odečteme z přechodové charakteristiky časový okamžik t1 a vypočteme součet časových konstant T1 a T2 podle vztahu:
- Vypočteme časový okamžik t2 podle vzorce:
- Z grafu přechodové charakteristiky odečteme hodnotu y(t2).
- Podle tabulky 1 určíme poměr časových konstant τ2, kde
- Ze známého součtu a poměru časových konstant vypočteme T1 a T2
| y(t2) | τ2 | y(t2) | τ2 |
|---|---|---|---|
| 0,30 | 0,000 | 0,22 | 0,183 |
| 0,29 | 0,023 | 0,21 | 0,219 |
| 0,28 | 0,043 | 0,20 | 0,264 |
| 0,27 | 0,063 | 0,19 | 0,322 |
| 0,26 | 0,084 | 0,18 | 0,403 |
| 0,25 | 0,105 | 0,17 | 0,538 |
| 0,24 | 0,128 | 0,16 | 1,000 |
| 0,23 | 0,154 |
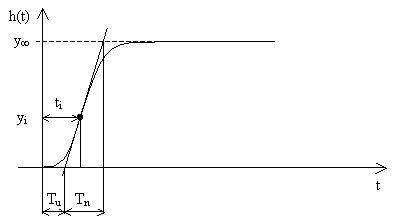
Obr. 5 Aproximace proporcionální soustavou 2.řádu se stejnými časovými konstantami
| Parametry přenosu | 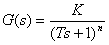 |
určíme následujícím postupem: |
- Přechodovou charakteristiku normujeme vzhledem k ustálené hodnotě y(¥).
- Sestrojíme tečnu v inflexním bodě a určíme τ podle vztahu:

- Podle hodnoty τ určíme z tab. 2 nejbližší vyšší řád n aproximační soustavy a souřadnici inflexního bodu yi.
- Pomocí yi určíme v grafu přechodové charakteristiky inflexní bod a odečteme souřadnici ti.
- Hodnotu časové konstanty T určíme ze vztahu:
kde ti - souřadnice času v inflexním bodě přechodové charakteristiky, Td - časová konstanta dopravního zpoždění, n - řád aproximační soustavy.
, resp. 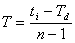
pro Td > 0
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| τ | 0,104 | 0,218 | 0,319 | 0,41 | 0,493 | 0,57 | 0,642 | 0,709 | 0,773 |
| yi | 0,264 | 0,327 | 0,359 | 0,371 | 0,384 | 0,394 | 0,401 | 0,407 | 0,413 |
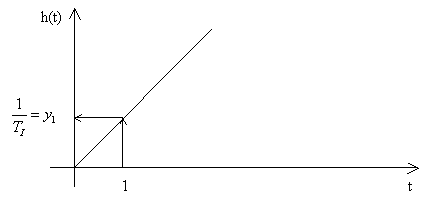
Obr. 6 Vyhodnocení přechodové charakteristiky integrační soustavy
kde TI - časová konstanta.
Jediný parametr přenosu TI určíme z přechodové charakteristiky z hodnoty y1, kterou odečteme pro časový okamžik t = 1. TI se pak vypočte:

Obr. 7 Vyhodnocení přechodové charakteristiky integrační soustavy se setrvačností
jehož parametry stanovíme následujícím postupem: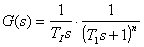
- Z grafu přechodové charakteristiky odečteme hodnoty t0, y(t0), 1/TI
- Vypočteme pomocnou konstantu A:
- Z tabulky 3 určíme řád systému n podle konstanty A.
- Vypočteme hodnotu časové konstanty T1:
| n | 1 | 2 | 3 | 4 |
| A | 0,368 | 0,271 | 0,224 | 0,195 |
 Obr. 8 Skoková změna vstupního signálu |
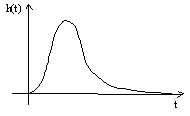 Obr. 9 Přechodová charakteristika derivačního členu |
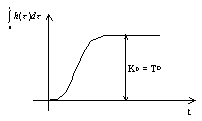 Obr. 10 Zintegrovaná přechodová charakteristika derivačního členu |
kde TD - derivační časová konstanta, Ti - i-tá časová konstanta, i - proměnná vyjadřující pořadová čísla časových konstant, n - proměnná vyjadřující pořadové číslo poslední časové konstanty.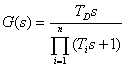
Přechodová charakteristika pro čas t → ¥ nabývá hodnotu y(¥) = 0. Integrujeme-li přechodovou charakteristiku, můžeme ji považovat za odezvu proporcionálního systému na skokovou změnu u0.
Integrací dostaneme: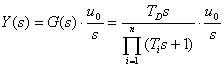
Získanou odezvu lze popsat pomocí proporcionálního členu: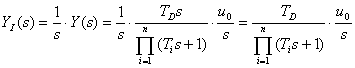
jehož konstanty určíme některým z dříve uvedených postupů.
 Obr. 11 Skoková změna vstupního signálu |
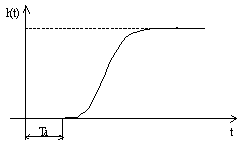 Obr. 12 Přechodová charakteristika soustavy s dopravním zpožděním |
kde G1(s) - přenos soustavy bez dopravního zpoždění, e - Eulerovo číslo, Td - časová konstanta dopravního zpoždění.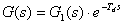
Nejdříve určíme přenos soustavy bez dopravního zpoždění G1(s) a pak určíme
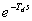 .
.
Toho se využívá u metod, které nepočítají s dopravním zpožděním.
Konstanty tohoto obrazového přenosu se stanoví pomocí níže uvedených metod.
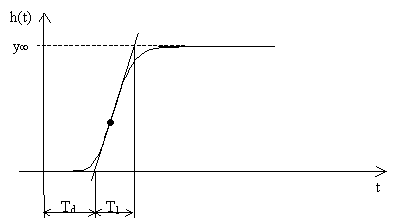
Obr. 13 Aproximace přechodové charakteristiky pomocí tečny v inflexním bodě
Takto získané hodnoty parametrů dosadíme do obrazového přenosu ve tvaru: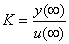
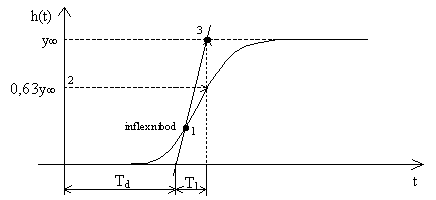
Obr. 14 Aproximace přechodové charakteristiky pomocí sečny v inflexním bodě
| Parametry přenosu | 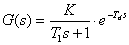 |
určíme následujícím způsobem: |
- Stanovíme inflexní bod 1.
- Určíme hodnotu 0,63y¥. Vyznačíme ji na přechodové charakteristice (bod 2) a najdeme pro tento časový okamžik bod 3 na pořadnici ustáleného stavu y¥.
- Přímka procházející body 1 a 3 vytne na časové ose okamžik, který definuje dopravní zpoždění Td a časovou konstantu T1. Zesílení K vypočteme podle známého vztahu:
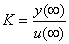
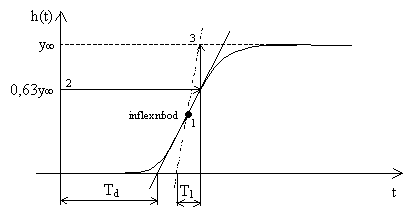
Obr. 15 Aproximace přechodové charakteristiky pomocí tečny a sečny v inflexním bodě
| Parametry přenosu | 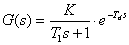 |
určíme následujícím postupem: |
- Nalezneme inflexní bod 1, v němž sestrojíme tečnu.
- Určíme hodnotu 0,63y¥. Vyznačíme ji na přechodové charakteristice a najdeme pro tento časový okamžik bod 3 na pořadnici ustáleného stavu y¥.
- Přímka procházející body 1 a 3, resp. časovou osou t a bodem 3 definuje časovou konstantu T1. Průsečík tečny procházející inflexním bodem s časovou osou t určuje časovou konstantu dopravního zpoždění Td. Zesílení K se vypočte podle vztahu:
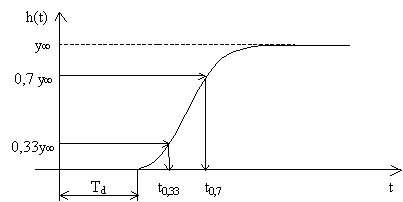
Obr. 16 Aproximace přechodové charakteristiky dvoubodovou metodou - varianta č. 1
| Parametry přenosu | 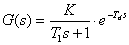 |
určíme takto: |
- Stanovíme hodnoty y0,7 = 0,7.y(¥), y0,33 = 0,33.y(¥) a jim odpovídající časové okamžiky t0,7 a t0,33.
- Z hodnot t0,7 a t0,33 vypočteme parametry přenosu podle vztahů:
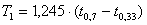
- Zesílení K se vypočte podle vztahu:
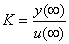
Obr. 17 Aproximace přechodové charakteristiky dvoubodovou metodou - varianta č. 2
| Parametry přenosu | 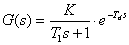 |
určíme takto: |
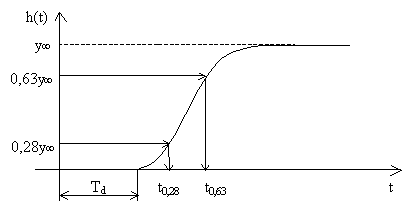
- Stanovíme hodnoty y0,63 = 0,63.y(¥), y0,28 = 0,28.y(¥) a jim odpovídající časové okamžiky t0,63 a t0,28.
- Z hodnot t0,63 a t0,28 vypočteme parametry přenosu podle vztahů:
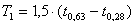
- Zesílení K se vypočte podle vztahu:
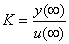
Abychom stanovili parametry přenosu, postupuje následovně: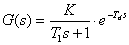
- Zjistíme časové konstanty t0,33 a t0,7 pro 33% a 70% ustálené hodnoty odezvy systému.
- Konstanty modelu určíme podle následujících vzorců:
jehož parametry určíme následovně: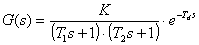
- Stanovíme časové konstanty pro 9%, 26% a 70% ustálené hodnoty odezvy systému t0,09, t0,26 a t0,7.
- Časovou konstantu dopravního zpoždění vypočteme podle vzorce:
- Vypočteme koeficienty B a C podle vzorců:
- Vypočteme časové konstanty T1, T2 a zesílení K podle vztahů:
Zesílení K spočítáme podle známého vztahu:
Koeficienty polynomu ve jmenovateli přenosu vypočteme následujícím způsobem: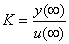
- Vypočteme tzv. momenty Mi podle vzorce:
kde i - index.
Počet momentů musí být roven i řádu náhradního modelu n.
- Pomocí momentů se následně vypočítají plochy Si. Jakmile vyjde plocha Si záporná, je nutné výpočet ukončit. Maximální řád modelu je pak určen řádem ještě kladné hodnoty plochy Si.
.
.
.
- Vypočteme koeficienty ai:
Pokud přechodovou charakteristiku před použitím této metody znormujeme, tzn. vydělíme nejvyšší naměřenou hodnotou, pak bude K = 1 a tudíž vypočtená plocha Si bude přímo koeficient ai.