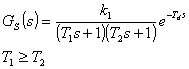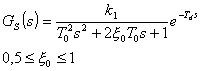4 Syntéza lineárních regulačních obvodů
Syntézou lineárních regulačních obvodů se myslí nejen navržení struktury obvodu, ale i jeho parametrů. Přičemž takto navržený obvod, musí splňovat požadavky kladené na jeho regulaci.
Tato kapitola se bude zabývat syntézou klasických regulačních obvodů, které lze rozdělit na dvě hlavní části: regulátor a regulovanou soustavu.
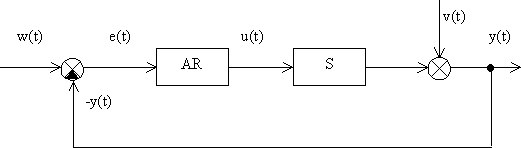
Obr. 4-1 Regulační obvod s analogovým regulátorem
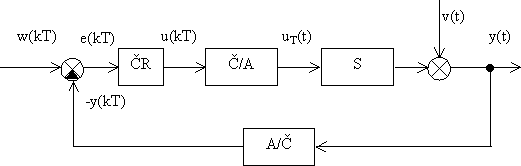
Obr. 4-2 Regulační obvod s číslicovým regulátorem
Syntézou se potom myslí volba vhodného regulátoru k zadané soustavě a jeho seřízení podle určitého kritéria.
Při syntéze regulačního obvodu musíme znát:
a) Dynamické vlastnosti soustavy
b) Předpokládaný průběh řídicí nebo poruchové veličiny a místo jejího vstupu do regulované soustavy (řídicí veličina je většinou konstantní, úkolem regulace je kompenzovat měnící se poruchové veličiny. Vstupní funkcí ve většině případů je jednotkový skok.)
c) Požadavky na kvalitu regulace
Bude zde ukázána metoda inverze dynamiky. Tato metoda je jednoduchá a dostatečně přesná.
4.1 Metoda inverze dynamiky
Výhoda této metody [Vítečková 2000] spočívá ve snadném a rychlém seřízení standardních typů analogových a číslicových regulátorů pro základní druhy regulovaných soustav. Soustavy mohou být bez dopravního zpoždění nebo s dopravním zpožděním.
Typ regulátoru je doporučen z hlediska vlastností regulované soustavy a požadavku na nulovou regulační odchylku způsobenou skokovou změnou polohy žádané veličiny w, resp. poruchy v působící na výstupu regulované soustavy.
Budeme předpokládat, že regulované soustavy mají některý z následujících náhradních L-přenosů:
|
|
(4.1) |
|
|
(2.2) |
|
|
(4.3) |
|
|
(4.4) |
|
|
(4.5) |
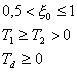
kde
|
|
- |
koeficient přenosu (rozměr = podíl rozměrů výstupní a vstupní veličiny, u integračních regulovaných soustav je nutno tento rozměr vynásobit čas-1) |
|
|
- |
netlumený úhlový kmitočet (čas-1) |
Pokud regulovaná soustava nemá ani jeden z výše uvedených tvarů, je nutné ji aproximovat. Postup aproximace regulovaných soustav náhradními přenosy je popsán viz [Vítečková 2000].
Dále budeme předpokládat, že budou použity pouze
standardní typy analogových a číslicových regulátorů. Vycházíme z jejich značné
univerzality a velkým rozšířením v technické praxi. Potom jsou doporučené
regulátory konvenčního typu a trvalá regulační odchylka ![]() způsobená skokovou
změnou žádané veličiny w je nulová.
Rovněž i trvalá regulační odchylka
způsobená skokovou
změnou žádané veličiny w je nulová.
Rovněž i trvalá regulační odchylka ![]() způsobená skokovou
změnou poruchy v je nulová za
předpokladu, že porucha působí na výstupu regulované soustavy.
způsobená skokovou
změnou poruchy v je nulová za
předpokladu, že porucha působí na výstupu regulované soustavy.
U regulovaných soustav s dopravním zpožděním se
při seřízení regulátoru vychází
z požadovaného relativního překmitu ![]() . Při mezním aperiodickém průběhu je
. Při mezním aperiodickém průběhu je ![]() a je minimalizována
lineární regulační plocha viz [Vítečková 2000].
a je minimalizována
lineární regulační plocha viz [Vítečková 2000].
Nejprve je třeba vyjádřit vlastnosti regulované soustavy některým ze základních tvarů L-přenosů. Pak na základě tabulky 4.1 určíme pro danou regulovanou soustavu typ regulátoru a optimální hodnoty jeho stavitelných parametrů. Je zapotřebí uvažovat dva případy:
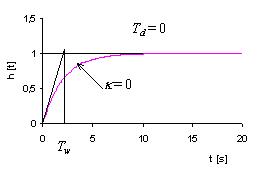
![]() .
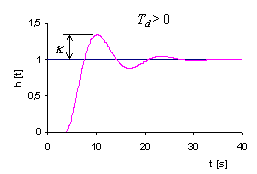
.
a) |
b) |
Obr. 4-3
Tab. 4-1
|
|
REGULOVANÁ SOUSTAVA |
REGULÁTOR |
ANALOGOVÝ T = 0 ČÍSLICOVÝ T > 0 |
||||
|
TYP |
|
|
|
||||
|
|
|
||||||
|
1 |
|
P |
|
|
- |
- |
|
|
2 |
|
PI |
|
|
|
- |
|
|
3 |
|
PD |
|
|
- |
|
|
|
4 |
|
PID |
|
|
|
|
|
|
5 |
|
PID |
|
|
|
|
|
Tab. 4-2
|
|
0 |
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,35 |
0,40 |
0,45 |
0,50 |
|
|
1,282 |
0,984 |
0,884 |
0,832 |
0,763 |
0,697 |
0,669 |
0,640 |
0,618 |
0,599 |
0,577 |
|
|
2,718 |
1,944 |
1,720 |
1,561 |
1,437 |
1,337 |
1,248 |
1,172 |
1,104 |
1,045 |
0,992 |
V tab. 4.1 je:
![]() .
.
Pro T > 0 tabulka 4.1 platí pro číslicové regulátory, pro T = 0 platí pro analogové regulátory.
V případě, kdy dopravní zpoždění ![]() , se nejdříve na základě požadovaného relativního překmitu
, se nejdříve na základě požadovaného relativního překmitu ![]() u přechodové
charakteristiky
u přechodové
charakteristiky ![]() uzavřeného
regulačního obvodu (obr. 4.3b) a (tab. 4.2) určí koeficient
uzavřeného
regulačního obvodu (obr. 4.3b) a (tab. 4.2) určí koeficient
![]() .
.
Pak teprve z (tab. 4.1) určíme optimální hodnoty
stavitelných parametrů doporučeného regulátoru. Pokud dopravní zpoždění ![]() je velmi malé,
hodnotu určeného koeficientu a je
třeba vhodně snížit s ohledem na omezení akční veličiny a maximální
nastavitelnou hodnotou zesílení regulátoru
je velmi malé,
hodnotu určeného koeficientu a je
třeba vhodně snížit s ohledem na omezení akční veličiny a maximální
nastavitelnou hodnotou zesílení regulátoru ![]() .
.
V případě ![]() určíme hodnoty
stavitelných parametrů přímo z (tab. 4.1) pro daný typ regulované soustavy.
Požadovaný průběh přechodové charakteristiky
určíme hodnoty
stavitelných parametrů přímo z (tab. 4.1) pro daný typ regulované soustavy.
Požadovaný průběh přechodové charakteristiky ![]() uzavřeného
regulačního obvodu se v tomto případě předpokládá podle (obr. 4.3a).
Časová konstanta
uzavřeného
regulačního obvodu se v tomto případě předpokládá podle (obr. 4.3a).
Časová konstanta ![]() musí být zvolena
s ohledem na omezení akční veličiny a maximální nastavitelnou hodnotou
regulátoru
musí být zvolena
s ohledem na omezení akční veličiny a maximální nastavitelnou hodnotou
regulátoru ![]() , u regulačního obvodu s číslicovým regulátorem musí
platit
, u regulačního obvodu s číslicovým regulátorem musí
platit ![]() .
.
4.2 Příklady
Příklad 1)
Pro regulovanou soustavu
s přenosem GS(g
) určete vhodný
analogový i číslicový regulátor a
seřiďte jej tak, aby přechodová charakteristika ![]() vykazovala překmit
kolem
vykazovala překmit
kolem ![]() .
.
![]() ;
;
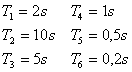
Řešení:
Převedeme zadaný přenos regulované soustavy na jeden ze základních tvarů uvedených v (tab. 4.1).
Volíme tvar:
![]()
pro převedení použijeme postupu uvedeném ve [Vítečková 2000]:
![]()
pak náhradní přenos je:
![]()
Z (tab. 4.1) je patrné, že pro naši soustavu je vhodný PID regulátor. Výpočet optimálních hodnot stavitelných parametrů PID regulátoru provedeme na základě vztahů opět podle (tab. 4.1).
Výpočet stavitelných parametrů pro PID regulátor:
a) analogový regulátor:
U analogového regulátoru uvažujeme ![]() .
.
Pro relativní překmit ![]() z (tab. 4.2) odečteme
příslušnou hodnotu a
a b:
z (tab. 4.2) odečteme
příslušnou hodnotu a
a b:
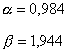
potom:
![]()
Optimální hodnoty stavitelných parametrů určíme podle (tab. 4.1)
![]()
![]()
![]()
b) číslicový regulátor:
Velikost vzorkovací periody volíme tak, aby byla splněna
podmínka ![]() :
:
![]()
zvolíme velikost vzorkovací periody ![]() .
.
Hodnoty a a b jsou stejné jako pro analogový regulátor:
![]()
optimální hodnoty stavitelných parametrů určíme podle (tab. 4.1):
![]()
![]()
![]()