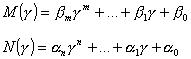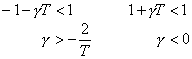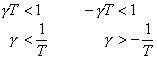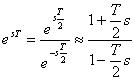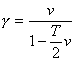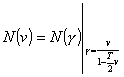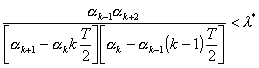3 Stabilita lineárních dynamických systémů
Stabilita lineárních dynamických systémů je především
vlastnost těchto systémů.
Stabilitu lze definovat: lineární
dynamický systém je stabilní právě tehdy, když na omezený vstupní signál
dostaneme omezený výstupní signál.
Pro odvození podmínky stability vycházíme z lineární diferenční rovnice:
|
|
(3.1) |
Uvažujeme nulové počáteční podmínky.
Po D-transformaci rovnice (3.1) obdržíme:
|
|
(3.2) |
Po úpravě:
|
|
(3.3) |
D-přenos má potom tvar:
|
|
(3.4) |
Obraz řešení má tvar:
|
|
|
|
kde |
|
Jak již bylo dříve zmíněno, stabilita je schopnost systému vrátit se do rovnovážného stavu po odeznění vstupního signálu u(kT). Proto nemá pravá strana vliv na stabilitu. Z tohoto důvodu nás bude zajímat pouze řešení homogenní delta diferenční rovnice:
|
|
(3.5) |
Po D-transformaci rovnice (3.5) obdržíme:
|
|
(3.6) |
tzv. charakteristickou rovnici
(charakteristický polynom), kde kořeny ![]() rozhodují o stabilitě
řešení delta rovnice.
rozhodují o stabilitě
řešení delta rovnice.
Obecné řešení rovnice (3.5) má tvar:
|
|
(3.7) |
Systém je stabilní právě tehdy, když kořeny charakteristické
rovnice leží uvnitř jednotkové kružnice. Tato podmínka platí pro ![]() , jestliže
, jestliže
|
|
(3.8) |
což je nutná a postačující podmínka stability.
Jejím vyřešením obdržíme grafické znázornění oblasti stability:
|
|
|
|
reálná část |
imaginární část |
|
|
|
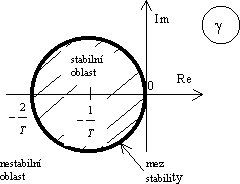
Obr. 3-1 Stabilní a nestabilní oblast
Z obrázku je patrné, že
diskrétní lineární systém je stabilní, leží-li všechny kořeny charakteristické
rovnice (3.6) uvnitř kružnice o poloměru ![]() se středem
v bodě
se středem
v bodě ![]() .
.
3.1 Bilineární transformace
Abychom mohli použít algebraická kritéria stability pro spojité dynamické systémy, jako např. Hurwitzovo kritérium, musíme pomocí bilineární transformace převést stabilní oblast komplexní roviny gna stabilní oblast nové komplexní proměnné v. Jedná se zde o tzv. bilineární transformaci, která převede kružnici v komplexní rovině g na imaginární osu v a vnitřek kružnice v komplexní roviněg na levou polorovinu komplexní roviny v, viz (obr. 3-2)
Odvození výrazu pro bilineární transformaci [Boháč 1996]:
Srovnáním vztahů (1.2) a (1.9) obdržíme následující vztah:
|
|
(3.9) |
Provedeme Padého rozvoj
exponenciální funkce ![]() s tím, že budeme
uvažovat pouze první dva členy:
s tím, že budeme
uvažovat pouze první dva členy:
|
|
(3.10) |
Po úpravách a zavedené substituci s = v, obdržíme:
|
|
(3.11) |
Pomocí bilineární transformace
transformujeme ![]()
|
|
(3.12) |
pro kterou platí nutná a postačující podmínka stability
|
|
(3.13) |
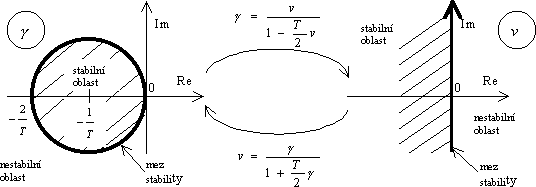
Obr. 3-2 Bilineární transformace
Po převedení stabilní oblasti pomocí bilineární transformace lze využít všechna známá kritéria pro kontrolu stability spojitých systémů. Tato kritéria nám umožňují rozhodnout o stabilitě regulačního obvodu (systému) bez výpočtu jeho pólů, resp. charakteristických čísel. Rozlišujeme algebraická a kmitočtová kritéria stability. Zde popíšeme dvě algebraická kritéria stability – Hurwitzovo kritérium stability a Routhovo-Schurovo kritérium stability.
Závěry [Balátě 1987], které přímo můžeme provést z daného tvaru charakteristické rovnice uzavřeného regulačního obvodu:
|
|
(3.14) |
1.
Nutnou podmínkou
stability dynamických systémů je, aby koeficienty ![]() charakteristické
rovnice existovaly a měly stejné znaménko (Stodolova podmínka)
charakteristické
rovnice existovaly a měly stejné znaménko (Stodolova podmínka)
2. Je-li charakteristická rovnice 2. řádu a všechny tři koeficienty jsou stejného znaménka, potom je systém vždy stabilní. První podmínka přechází v nutnou a postačující podmínku stability
3. Je-li charakteristická rovnice vyššího stupně než druhého a všechny koeficienty jsou nenulové a stejného znaménka, je stabilita dynamického systému závislá na velikosti jednotlivých koeficientů. Stabilita se potom musí řešit pomocí některého kritéria stability.
3.2 Algebraická kritéria stability
Tato kritéria vycházejí z charakteristické rovnice dynamického systému, resp. z charakteristického polynomu dynamického systému. Pomocí těchto kritérií můžeme rozhodnout, zda systém je stabilní nebo není stabilní, ale nedávají nám informaci do jaké míry je systém tlumený. Kritéria nemůžeme použít při vyšetřování stability systémů s dopravním zpožděním. Mezi algebraická kritéria stability řadíme Hurwitzovo kritérium a Routhovo-Schurovo kritérium.
3.2.1 Hurwitzovo kritérium stability
Velmi jednoduché kritérium. Je vhodné pro dynamické systémy, jejichž charakteristický polynom je nejvýše pátého stupně.
Pro toto kritérium platí:
1. Nutná Stodolova podmínka
všechny koeficienty charakteristické rovnice (3.14) musí být kladné
|
ai>0 |
pro i = 0,1,…,n |
(3.15) |
2. Nutná a postačující podmínka: hlavní rohové subdeterminanty Hi pro i = 2,3,…,n-1 musí být kladné
|
Hi>0 |
pro i = 2,3,…,n-1 |
(3.16) |
kde
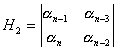 ,
,
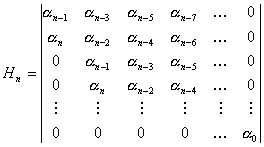
ai
jsou koeficienty charakteristického polynomu N(v)
![]()
3.2.2 Routhovo-Schurovo kritérium stability
Lze použít pro dynamické systémy, s libovolným stupněm charakteristického polynomu.
Postup:
1. Koeficienty charakteristického polynomu (3.14) vypíšeme vedle sebe od nejvyšší mocniny.
2.
Každý druhý koeficient (an-1,
an-3,...) podtrhneme
a vynásobíme podílem prvních dvou koeficientů ![]() . Výsledek napíšeme o jeden koeficient vlevo pod
předcházející řadu.
. Výsledek napíšeme o jeden koeficient vlevo pod
předcházející řadu.
3. Tuto řadu koeficientů odečteme od předchozí a získáme novou řadu, která má o jeden koeficient méně.
4. Jsou-li všechny koeficienty nové posloupnosti kladné, opakujeme postup od bodu 2.
5. Je-li v nové řadě aspoň jeden koeficient záporný, výpočet ukončíme, neboť charakteristická rovnice má nestabilní kořen a systém je nestabilní.
6. Je-li aspoň jeden koeficient nulový, výpočet ukončíme, neboť charakteristická rovnice má nulový kořen a systém je na mezi stability.
7. Výše zmíněný postup opakujeme až k řadě tří koeficientů. Jsou-li koeficienty kladné, charakteristický polynom má stabilní kořeny a systém je stabilní.
Routhova-Schurova tabulka:
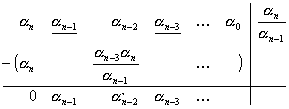 , kde
, kde ![]()
3.3 Přímá kontrola pomocí podmínek
Způsob kontroly stability pomocí bilineární transformace a následného použití některého z kritérií známých pro kontrolu stability u spojitých systémů může být někdy zdlouhavý. Týká se to případů, kdy charakteristický polynom je vyššího řádu. Např. Hurwitzovo kritérium je pro vyšší řády nevhodné. Z těchto důvodů se hledaly způsoby přímé kontroly stability. [Petrov 1986] uvádí 3 podmínky, pomocí kterých lze přímo kontrolovat stabilitu lineárních delta diferenčních rovnic.
Lineární delta diferenční rovnice má tvar:
|
|
(3.17) |
Podle Petrova postačujícími podmínkami stability diskrétních systémů se vzorkovací periodou T, popsaných výše uvedenou rovnicí, jsou následující 3 podmínky:
|
1. |
pro |
(3.18) |
|
2. |
pro |
(3.19) |
|
3. |
|
(3.20) |
kde l* je kořen rovnice ![]()
Pro ![]() se podmínky stability (3.18)-(3.20) diskrétních dynamických
systémů stávají postačujícími podmínkami stability spojitých systémů.
se podmínky stability (3.18)-(3.20) diskrétních dynamických
systémů stávají postačujícími podmínkami stability spojitých systémů.
Tyto podmínky lze zároveň použít pro volbu vzorkovací periody T, při přechodu od spojitých dynamických systémů na diskrétní dynamické systémy.
3.4 Příklady
Příklad 1) Nutná a postačující podmínka stability
Zjistěte, zda
dynamický systém daný přenosem je
stabilní pro ![]() .
.
![]()
Řešení:
Dosadíme ![]() :
:
![]()
Charakteristický polynom je:
![]()
kořeny charakteristického polynomu jsou:
![]()
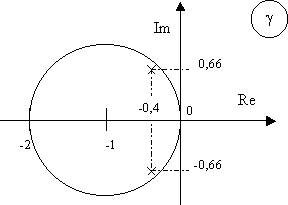
Obr. 3-3 Stabilní oblast
Z obrázku (Obr. 3-3) je patrné, že kořeny leží uvnitř jednotkové kružnice. Z toho vyplývá, že zadaný systém je stabilní.
Příklad 2) Hurwitzovo kritérium stability
Zjistěte, zda
dynamický systém daný přenosem je
stabilní pro ![]() .
.
|
|
(3.21) |
Řešení:
Dosadíme ![]() :
:
![]()
Nyní určíme výsledný tvar charakteristického polynomu:
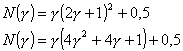
![]()
Po provedení bilineární transformace a dosazením ![]() dostaneme:
dostaneme:
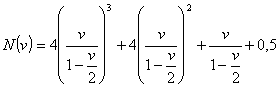
![]()
Po úpravě má charakteristický polynom tvar:
![]()
Aby systém byl stabilní, musí být splněny dvě podmínky:
Stodolova podmínka (nutná podmínka stability):
![]()
Pro náš případ:
![]()
Z toho vyplývá, že Stodolova podmínka je splněna.
Z Hurwitzova kritéria (3.16) vyplývá:
![]()
Pro náš případ stačí určit ![]() :
:
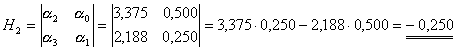
Protože hodnota
subdeterminantu ![]() není kladná, podmínka není splněna a systém je tedy
nestabilní.
není kladná, podmínka není splněna a systém je tedy
nestabilní.
Příklad
3) Routhovo-Schurovo kritérium stability
Určete
pomocí
Routhova-Schurova kritéria, zda dynamický systém daný přenosem (3.21) je stabilní.
Řešení:
Pro zjištění, zda systém je stabilní, potřebujeme určit charakteristický polynom N(g), který poté transformujeme na charakteristický polynom N(v) - postupujeme stejným způsobem jako v předchozím příkladu, kde jsme došli k závěru, že transformovaný charakteristický polynom N(v) má tvar:
![]()
Nyní vypíšeme koeficienty charakteristického polynomu od nejvyšší mocniny vedle sebe a sestavíme Routhovu-Schurovu tabulku podle výše uvedeného postupu:
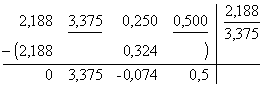
Protože nám vyšel jeden koeficient záporný (-0,074), systém je nestabilní a výpočet ukončíme.
Příklad 4) Přímá kontrola pomocí podmínek
Zjistěte, zda dynamický systém daný přenosem je stabilní pro ![]() .
.
|
|
(3.22) |
Řešení:
Z přenosu určíme koeficienty ![]() :
:
![]()
Koeficienty dosadíme do podmínek (3.18),(3.19) a (3.20), kde
![]() :
:
Podmínka (3.18):
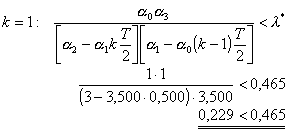
Podmínka je splněna.
Podmínka (3.19):
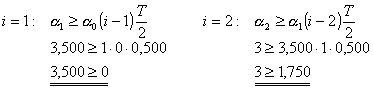
Podmínka je splněna.
Podmínka (3.20):
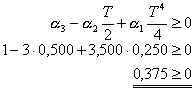
Podmínka je splněna.
Protože všechny tři podmínky jsou splněny, regulační obvod je stabilní.
Příklad 5)
Zjistěte, zda dynamický systém daný přenosem (3.22) je stabilní pomocí Hurwitzova kritéria stability a Routhova-Schurova kritéria stability.
Řešení:
Charakteristický polynom N(v) má tvar:
![]()
Po provedení bilineární transformace a úpravě dostaneme:
|
|
(3.23) |
a) Hurwitzovo kritérium stability:
Splnění Stodolovy podmínky:
![]()
Stodolova podmínka je splněna.
Z Hurwitzova kritéria (3.16) vyplývá:
Pro náš případ stačí určit H2:
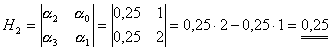
Hodnota subdeterminantu H2 je kladná.
Protože jsou obě podmínky Hurwitzova kritéria stability splněny, systém je stabilní.
b) Routhovo-Schurovo kritérium stability:
Vypíšeme koeficienty charakteristického polynomu a sestavíme Routhovu-Schurovu tabulku podle výše uvedeného postupu.
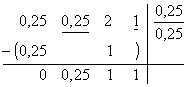
Protože nám vyšly všechny koeficienty kladné, systém je stabilní.