Návrh deadbeat regulátoru v prostředí Matlab

Metoda vychází z přenosové funkce regulované soustavy, která se získá ze spojitého popisu podle vztahu:

(přepočet s tvarovacím členem nultého řádu)

V programu Matlab to realizujeme příkazem C2D(num, den, Tv,’metoda přepočtu’). Pokud metodu přepočtu neuvádíme, automaticky je nastavena metoda ZOH tvarovací člen nultého řádu. Přenosová funkce regulované soustavy je potom ve tvaru:

Pro deadbeat regulátor je přenosová funkce uzavřeného obvodu ve tvaru

q1=a1q0 q2=a2q0	p1=b1q0 p2=b2q0	protože  odtud
........................................
qM=aMq0	pM=bMq0

Charakteristická rovnice diskrétního uzavřeného obvodu je:

má tedy M pólů v počátku z-roviny, regulovaná veličina za M kroků (M je řád soustavy) dosáhne žádanou hodnotu.

Pokud proces řízení obsahuje dopravní zpoždění, potom jsou koeficienty DB regulátoru určeny:

kde b_i jsou koeficienty čitatele pro i=1,2,…,M+d. Protože proces obsahuje dopravní zpoždění počet koeficientů je M+d. Prvních d koeficientů b_i bude nulových a od i=1+d jsou koeficienty nenulové. Z nulové hodnoty koeficientů čitatele diskrétního procesu je zřejmé, že nulové budou také koeficienty jmenovatele regulátoru procesu p_i, pro i=1,2,…,d a hodnoty koeficientů polynomu jmenovatele A od I=M+1 až po i=M+d.

Tedy koeficienty:

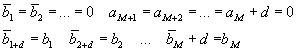
Struktura DB regulátoru představuje speciální typ diskrétního regulátoru ve tvaru:

Výstupní regulovaná veličina dosáhne žádanou hodnotu referenční proměnné w(k) za M+d kroků (kde d je dopravní zpoždění, které se z spojitého dopravního zpoždění určí vztahem d=D/T a T_v je perioda vzorkování) tj.

(ustálená hodnota postoupnosti řídícího zásahu)

Charakteristická rovnice uzavřeného regulačního obvodu je:

Příklad:

Úkolem je určit koeficienty DB regulátoru přímo v programu Matlab na základě jednoduchých příkazů, zadaný regulovaný proces je spojitý a je popsaný přenosovou funkcí ve tvaru:

Řešení:

Prvním krok je zadání spojitého přenosu procesu a jeho přepočet do Z-oblasti

» cit=tf([2 1], 1)
Transfer function:
2 s + 1
  
» men1=tf(1,[10 1])
 
Transfer function:
    1
--------
10 s + 1 

» men2=tf(1,[7 1])
 Transfer function:
    1
-------
7 s + 1 

» men3=tf(1,[3 1])
 Transfer function:
    1
-------
3 s + 1 

» Gpd=cit*men1*men2*men3
 Transfer function:
         2 s + 1
----------------------------
210 s^3 + 121 s^2 + 20 s + 1 

Gpz=C2D(Gpd,4)
 Transfer function:
 0.06525 z^2 + 0.04793 z - 0.007505
------------------------------------
z^3 - 1.499 z^2 + 0.7041 z -0.09978
 Sampling time: 4

Protože proces obsahuje dopravní zpoždění D=4 a perioda vzorkování T_v=4 v z-oblasti bude dopravní zpoždění d=D/T_v=4/4=1, teda celá přenosová funkce procesu bude násobená z^-1 čím se posunou koeficienty čitatele o 1 řád. Ve výpočtech pro koeficienty regulátoru budou proto nulové koeficienty p(i) a to o tolik jaká je hodnota d. Pro náš případ d=1, tedy bude nulový první koeficient tj. p=(1)=0, ostatní koeficienty budou počítané z posunutých hodnot polynomu B.

Výběr čitatele a jmenovatele z přenosu regulovaného procesu

» [Bz, Az]=tfdata(Gpz,'v') %vyber citatele a jmenovatele  

Bz =    0       0.0653  0.0479  -0.0075 
Az =    1.0000 -1.4986  0.7041  -0.0998

Upozornění: Matlab indexuje první prvek v matice a nebo ve vektoru od jedné tj. Bz(1) a nezná Bz(0).

q0=1/sum(Bz)
q0 =
  9.4628 

q1=Az(2)*q0
q1 = 
  -14.1813 

q2=Az(3)*q0
q2 = 
  6.6627 

q3=Az(4)*q0
q3 = 
  -0.9442

p1=0
p1 = 
  0 

p2=Bz(2)*q0
p2 = 
  0.6175 

p3=Bz(3)*q0
p3 = 
  0.4536 

p4=Bz(4)*q0
p4 =
  -0.0710

Zadání polynomů regulátoru:

Q=[q0, q1, q2, q3]
Q =
  9.4628  -14.1813  6.6627  -0.9442 

P=[p1, p2, p3, p4]
P =        
  0  0.6175  0.4536  -0.0710

Před zadáním přenosu regulátoru můžme provést kontrolu správnosti výpočtů:

sum(P) % Kontrola spravnosti vypoctu 
ans =     1

sum(Q) % Kontrola ustaleneho stavu
ans =    1.0000

Přenos DB regulátoru bude mít následující tvar:

.

regd_DBa.m - programový modul pro návrh DB regulátorů (m-file)