Stabilita je vlastnost systému. Je jedním ze základních požadavků, které klademe na regulační obvod.
Regulační obvod je stabilní, jestliže po vychýlení regulačního obvodu z rovnovážného stavu a odstranění podnětu, který tuto odchylku způsobil, se regulační obvod během času vrátí do původního rovnovážného stavu. Jinak řečeno je stabilita vlastnost regulačního obvodu vrátit se do rovnovážného stavu, jestliže skončí působení vzruchu, který ho z rovnovážného stavu vyvedl.[Švarc, I. 1992]
Podle stability rozlišujeme tři typy systémů: stabilní, na mezi stability a nestabilní.
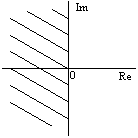
Nutná a postačující podmínka stability pro spojité systémy: regulační obvod je stabilní, leží-li všechny kořeny charakteristického polynomu v záporné polovině komplexní roviny (obr. 2.39).

obr. 2.39 Oblast stabilních kořenů pro spojité systémy
Nutná a postačující podmínka stability pro diskrétní systémy: systém je stabilní právě tehdy, když jsou kořeny charakteristického mnohočlenu v absolutní hodnotě menší než jedna (obr. 2.40).
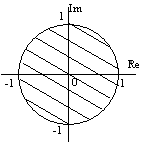
obr. 2.40 Oblast stabilních kořenů pro diskrétní systémy
Pro určení stability v programovém prostředí Matlab můžeme užít příkaz roots, pomocí něhož určíme hodnotu kořenů charakteristického polynomu. Na základě nutné a postačující podmínky stability, pak můžeme určit, zda jde o stabilní systém či nikoliv. Pomocí této podmínky určím pouze, zda je systém stabilní, pokud však není, nelze určit zda se jedná o systém na mezi stability nebo o systém nestabilní.
Pro spojité systémy je další možností Nyquistovo kriterium stability. Jedná se o kmitočtové kriterium, které rozhoduje o stabilitě regulačního obvodu na základě průběhu kmitočtové charakteristiky otevřené smyčky obvodu.
Podle Nyquistova kriteria musí pro stabilní obvod platit:
1. ![]()
2. ![]()
3. ![]()
Více informací naleznete v publikaci: Prezentační a výukový modul pro oblast analýzy regulačních obvodů.
Máme regulovanou soustavu zadanou přenosem GS(s), regulátor je typu PI zadaný přenosem GR(s) v obvodu je zapojen měřící člen s přenosem Gmč(s). Regulační obvod je zapojen podle obr. 2.41.
![]() ;
; ![]() ;
; ![]()
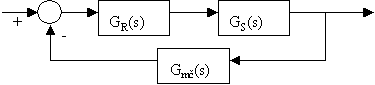
obr. 2.41 Zapojení regulačního obvodu
Nejdříve pomočí funkce tf zadáme jednotlivé přenosy:
R = tf([1],[5 0]); S = tf([5],[1 1]); mc =tf([1],[2 1]); |
Jednotlivé přenosy propojíme podle zadání a získáme přenos regulačního obvodu.
RS = series(R,S); sys = feedback (RS,mc) |
Nejdříve určíme stabilitu pomocí nutné a postačující podmínky stability, tedy pomocí kořenů charakteristického polynomu.
Pomocí příkazu tfdata určíme hodnotu charakteristického polynomu, která se nám načte do proměnné jmen.
[cit,jmen]=tfdata(sys,'v'); |
Kořeny polynomu pak zjistíme pomocí příkazu roots:
r = roots (jmen) r = -1.3982 -0.0509 + 0.5958i -0.0509 - 0.5958i |
Z výsledku vidíme, že se jedná o stabilní systém, neboť všechny reálné složky kořenů mají zápornou hodnotu:
Pro určení stability podle Nyquistova kriteria stability si nejdříve vypočítáme přenos otevřeného obvodu:
Go=series(RS,mc). |
Pomocí příkazu ltiview vykreslíme amplitudo fázovou kmitočtovou charakteristiku.
ltiview('nyquist',Go) |
Na výsledném grafu (obr. 2.42) vidíme že se jedná o stabilní systém neboť kmitočtová charakteristika protíná reálnou osu až za hodnotou –1.
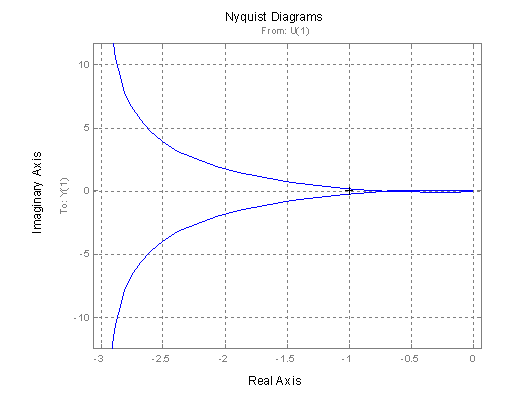
obr. 2.42 Kmitočtová charakteristika stabilního systému
Stabilitu můžeme určit i z logaritmické kmitočtové charakteristiky zadané pomocí příkazu ltiview:
ltiview('bode',Go) |
Na výsledném grafu (obr. 2.43) je vidět, že hodnota zesílení pro j=180° je menší než 0, jedná se tedy o stabilní systém.
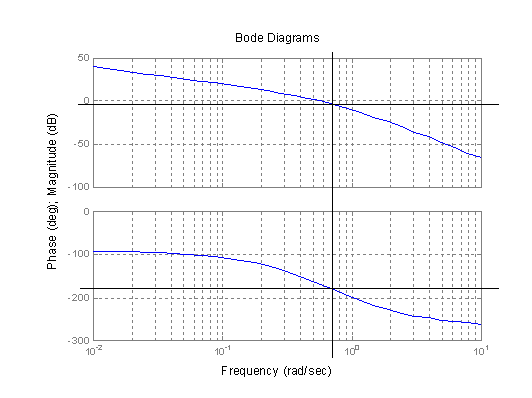
obr. 2.43 Logaritmická kmitočtová charakteristika stabilního systému
stab_ano.m - určení stability v probramu Matlab
Pro ověření stability v programu Simulink použijme bloky Step, Transfer Fnc, Sum a Scope zapojené podle schéma na obr. 2.44.
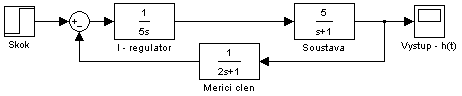
obr. 2.44 Zapojení bloků v programu Simulink
Výsledkem je přechodová charakteristika, na níž je vidět, jak se systém po určité době ustálí. Jedná se tedy o stabilní systém.
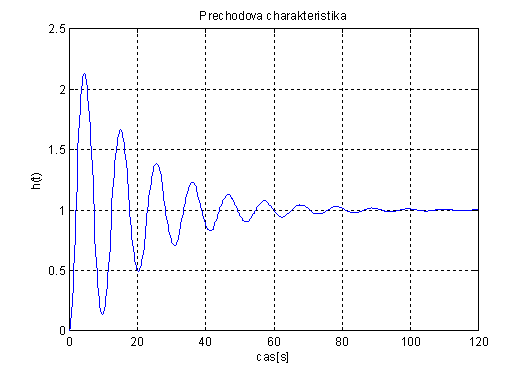
obr. 2.45 Přechodová charakteristika stabilního systému
sim_stab_ano.mdl - určení stability v probramu Simulink
Pro určení stability v tomto příkladu použijeme stejné zadání jako v předchozím případě pouze změníme hodnotu regulátoru na TI = 10/3.
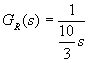 ;
; ![]() ;
; ![]()
Nejdříve zadáme přenos regulačního obvodu:
%nastaveni regulatoru TI = 10/3; R = tf([1],[TI 0]); %zadání soustavy a mc S = tf([5],[1 1]); mc =tf([1],[2 1]); %propojeni RS = series(R,S); sys = feedback (RS,mc) |
Použijeme stejný postup jako v předchozím příkladu:
[cit,jmen]=tfdata(sys,'v'); r1 = roots (jmen) r1 = -1.5000 0.0000 + 0.7071i 0.0000 - 0.7071i |
Z výsledku vidíme, že se jedná o nestabilní systém neboť pouze jeden kořen splňuje podmínku stability.
Nejdříve si určíme přenos otevřené smyčky Go(s):
|
Go=series(RS,mc); |
Pomocí následujícího příkazu nejdříve vykreslíme kmitočtovou charakteristiku:
|
ltiview('nyquist',Go) |
Z kmitočtové (obr. 2.46) charakteristiky vidíme, že se jedná o systém na mezi stability neboť charakteristika protíná reálnou osu v bodě –1.
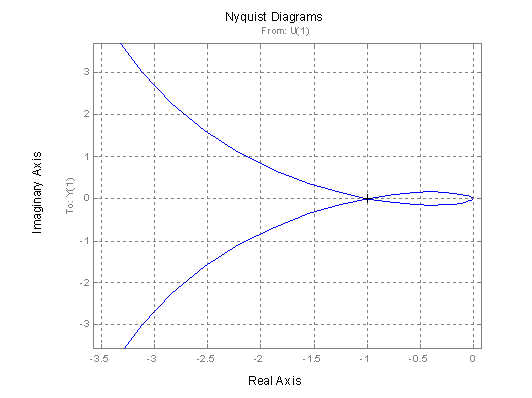
obr. 2.46 Kmitočtová charakteristika systému na mezi stability
Stabilitu lze určit i z logaritmické kmitočtové charakteristiky:
|
ltiview('bode',Go) |
Z výsledného grafu na obr. 2.47 vidíme, že jde o systém na mezi stability, neboť zesílení pro j=180° je rovno nule.
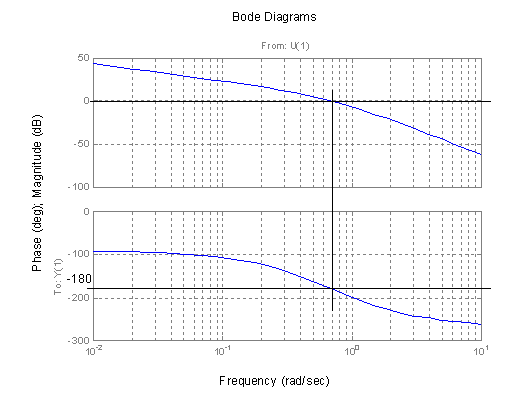
obr. 2.47 Logaritmická kmitočtová charakteristika systému na mezi stability
stab_mez.m - určení stability v probramu Matlab
Zapojení bloků je stejné jako v předchozím příkladě pouze se změní hodnota parametrů regulátoru.
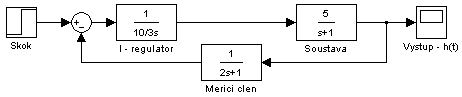
obr. 2.48 Zapojení bloků v programu Simulink
Na obr. 2.49 je vidět výsledná přechodová charakteristika systému na mezi stability, který kmitá s konstantní amplitudou.
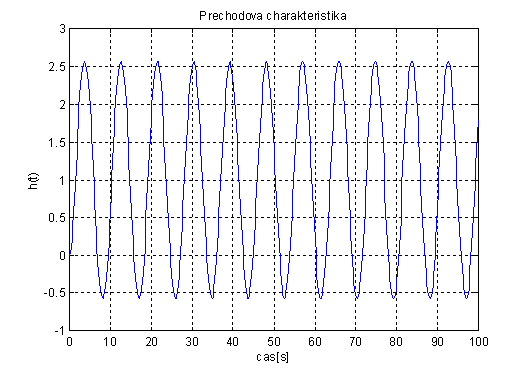
obr. 2.49 Přechodová charakteristika systému na mezi stability
sim_stab_mez.mdl - určení stability v probramu Simulink
Opět použijeme podobné zadání jako v předchozích případech. Změníme však hodnotu parametrů regulátoru na TI=2.
![]() ;
; ![]() ;
; ![]()
Nejdříve zadáme přenos jednotlivých prvků regulačního obvodu a propojíme je:
TI = 2 R = tf([1],[TI 0]) S = tf([5],[1 1]); mc =tf([1],[2 1]); RS = series(R,S); %propojení regulátoru a soustavy sys = feedback (RS,mc) %zapojení zpětné vazby a měřícího členu |
Použijeme stejný postup jako v předchozích příkladech:
[cit,jmen]=tfdata(sys,'v'); r1 = roots (jmen) r1 = -1.6545 0.0772 + 0.8658i 0.0772 - 0.8658i |
Z výsledku vidíme, že se jedná o nestabilní systém neboť dva kořeny mají reálné složky v kladné části komplexní roviny.
Nejdříve si určíme přenos otevřené smyčky Go(s):
Go=series(RS,mc); |
Pomocí následujícího příkazu nejdříve vykreslíme kmitočtovou charakteristiku:
ltiview('nyquist',Go) |
Z výsledné kmitočtové charakteristiky (obr. 2.50) vidíme, že se jedná o nestabilní systém, protože charakteristika protíná reálnou osu před bodem –1.
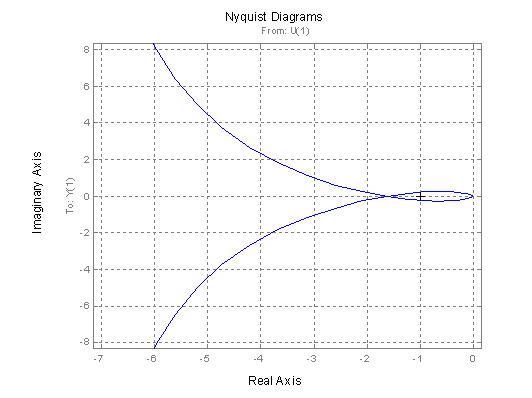
obr. 2.50 Kmitočtová charakteristika nestabilního systému
Pokud budeme stabilitu určovat z logaritmické kmitočtové charakteristiky použijeme příkaz:
ltiview('bode',Go) |
Na výsledném grafu (obr. 2.47) vidíme, že jde o systém nestabilní, neboť logaritmická amplituda pro j=180° je větší než nula.
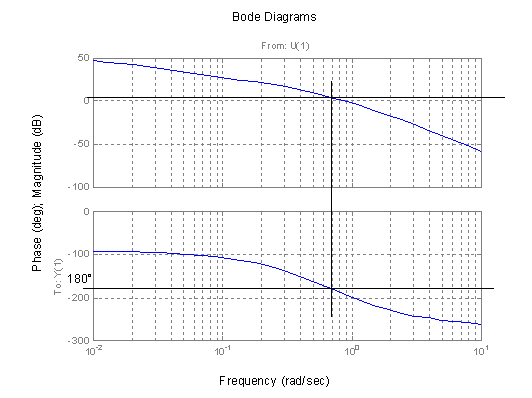
obr. 2.51 Logaritmická kmitočtová charakteristika nestabilního systému
stab_ne.m - určení stability v probramu Matlab
Zapojení bloků na obr. 2.52 je stejné jako v předchozích příkladech pouze se změní hodnota parametrů regulátoru.
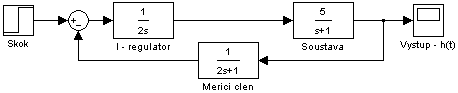
obr. 2.52 Zapojení bloků v programu Simulink
Na výsledné přechodové charakteristice (obr. 2.53) je dobře vidět, že se jedná o nestabilní systém, který se v čase neustálí, ale právě naopak se zvyšuje amplituda kmitů.
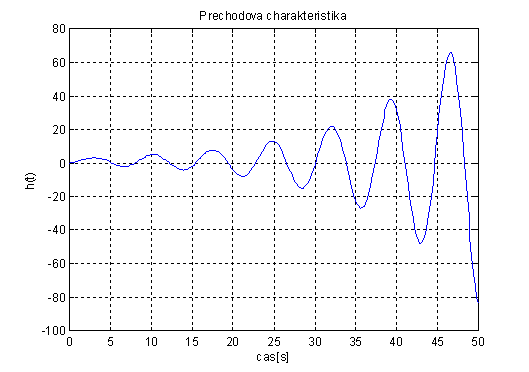
obr. 2.53 Přechodová charakteristika nestabilního systému
sim_stab_ne.mdl - určení stability v probramu Simulink