(9.1)
Na základě znalosti polohy pólů a nul (póly jsou kořeny mnohočlenu ve jmenovateli přenosu a nuly jsou kořeny mnohočlenu v čitateli přenosu) přenosu (4.1) v komplexní rovině s, lze určit vnější chování lineárních spojitých RO. Póly i nuly mohou být buď reálné, komplexně sdružené nebo ryze imaginární. Je-li přenos (4.1) dán ve tvaru, kdy polynomy čitatele i jmenovatele jsou rozloženy na součin kořenových činitelů, lze polohu pólů a nul v komplexní rovině určit přímo.
|
(9.1) |
kde jsou pi - póly systému, i=1,2,…,n, nj - nuly systému, j=1,2,…,m.
Záporně vzatým převráceným hodnotám reálných pólů a nul říkáme časové konstanty RO a označujeme je
|
(9.2) |
U pólů a nul je rozhodující jejich poloha vzhledem k imaginární ose (mez stability). V levé komplexní polorovině jsou stabilní póly a nuly (mají zápornou reálnou část), v pravé polorovině jsou nestabilní póly a nuly (mají kladnou reálnou část). Stabilní nula způsobuje překmit a nestabilní nula způsobuje podkmit přechodového pochodu. Nuly v počátku představují derivační charakter systému, póly v počátku naopak představují integrační charakter. Příčinou záporných reálných pólů je aperiodický přechodový jev. Komplexně sdružené póly způsobují kmitavý charakter přechodového děje. Čím jsou stabilní póly dále od imaginární osy, tím je přechodový děj více tlumen. Jsou-li nuly blíže imaginární ose než póly, bude převládat derivační charakter.
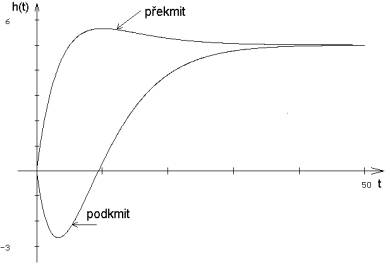
obr. 9.1 Zobrazení podkmitu a překmitu u přechodové charakteristiky