(8.19)
8.1.5 Nyquistovo kritérium stability
Je to kmitočtové kritérium, které rozhoduje o stabilitě RO na základě průběhu kmitočtové charakteristiky otevřeného regulačního obvodu. Tuto charakteristiku lze určit analyticky nebo experimentálně. Skutečnost, že při vyšetřování stability pomocí Nyquistova kritéria lze vycházet z experimentálně získaných hodnot, zvýhodňuje toto kritérium v porovnání s ostatními kritérii stability. Další výhodou je, že ho lze použít i pro RO s dopravním zpožděním (stejně jako Michajlovovo kritérium).
Charakteristická rovnice uzavřeného RO je dána vztahem
|
(8.19) |
Nyquistovo kritérium stability: "Je-li otevřený RO stabilní, pak uzavřený RO bude stabilní právě tehdy, když amplitudo-fázová kmitočtová charakteristika otevřeného regulačního obvodu Go(jw) neobklopuje kritický bod [-1, j0]" viz obr.8.4.
obr. 8.4. Příklady průběhů amplitudo-fázové kmitočtové charakteristiky stabilního otevřeného regulačního obvodu
Nyquistovo kritérium stability: "Je-li otevřený RO nestabilní a má p nestabilních kořenů, pak uzavřený RO bude stabilní právě tehdy, když amplitudo-fázová kmitočtová charakteristika otevřeného RO obklopí kritický bod [-1, j0] p/2 krát." viz. obr. 8.5.
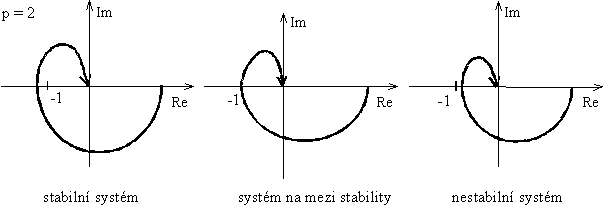
obr. 8.5. Příklady průběhů amplitudo-fázové kmitočtové charakteristiky nestabilního otevřeného regulačního obvodu
V případě, že určujeme stabilitu lineárních RO a otevřený RO je stabilní, můžeme použít analytické formulace Nyquistova kritéria. To spočívá v určení modulu a fáze kmitočtového přenosu otevřeného RO nebo v určení reálné a imaginární části kmitočtového přenosu otevřeného RO. Uzavřený RO bude stabilní právě tehdy, když
|
(8.20) |
resp.
|
(8.21) |
nebo
|
(8.22) |