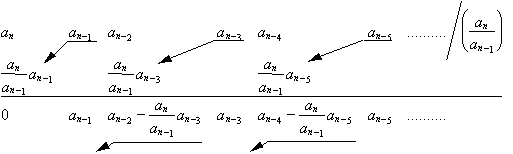8.1.3 Routhovo-Schurovo kritérium stability

Vycházíme opět z charakteristické rovnice ve tvaru (4.8). Podle daného algoritmu provádíme postupnou redukci charakteristické rovnice na rovnici nižšího stupně, až se dostaneme ke kvadratické rovnici. Podle Routhova-Schurova kritéria je RO stabilní právě tehdy, když při redukci se neobjeví záporné koeficienty a poslední tři koeficienty výsledné rovnice jsou kladné. Koeficienty napíšeme v řadě od nejvyšších nebo nejnižších mocnin a podtrhneme sudé koeficienty v pořadí. Každý sudý koeficient v pořadí násobíme podílem prvních dvou a napíšeme pod předcházející řadu posunutý o člen vlevo. Tuto výslednou řadu, která má členy vždy ob jeden předcházející řady, od ní odečteme. Výsledná řada koeficientů je pak o první člen kratší (stupeň předchozí rovnice se snížil o jednotku). Stejným postupem pokračujeme dále, až zbudou koeficienty rovnice druhého stupně - tři koeficienty.Výpočet lze znázornit schématem

.

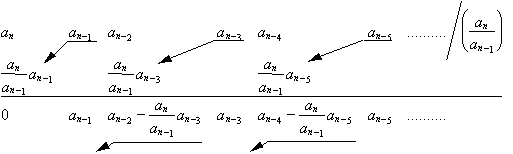(8.8)

Toto kritérium je účelné použít hlavně tehdy, když jsou koeficienty charakteristické rovnice vyjádřené číselně. Stodolova podmínka zůstává v platnosti a je podmínkou nutnou.