, Stodolova podmínka přechází v nutnou a postačující podmínku stability.
Jinak je nutno sestrojit z koeficientů charakteristické rovnice Hurwitzův
determinant n-tého stupně ve tvaru8.1.2 Hurwitzovo kritíérium stability
Vycházíme z charakteristické rovnice (4.8)
a platí zde tzv. Stodolova nutná podmínka stability, která zní: "Všechny
koeficienty charakteristické rovnice ai musí existovat a musí
mít stejné znaménko". Je-li charakteristický mnohočlen řádu
, Stodolova podmínka přechází v nutnou a postačující podmínku stability.
Jinak je nutno sestrojit z koeficientů charakteristické rovnice Hurwitzův
determinant n-tého stupně ve tvaru
 . |
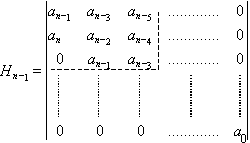(8.5) |
Hlavní rohové subdeterminanty jsou
 . |
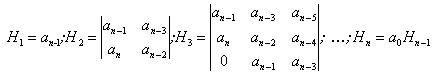(8.6) |
Podle Hurwitzova kritéria je RO stabilní právě tehdy, když hlavní rohové subdeterminanty jsou kladné,
 . |
(8.7) |
První a poslední rohový subdeterminant se počítat nemusí, protože je-li splněna Stodolova podmínka, jsou dané subdeterminanty vždy kladné. Pokud Hn-1=0, RO je na kmitavé mezi stability, tzn. charakteristická rovnice má dvojici ryze imaginárních kořenů. Je-li koeficient charakteristické rovnice a0=0 a všechny rohové subdeterminanty jsou kladné, RO je na nekmitavé mezi stability, tzn. charakteristická rovnice má nulový kořen.