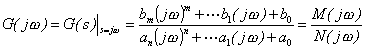3. Kmitočtové charakteristiky v logaritmických souřadnicích

3.1 Kmitočtový přenos

Kmitočtový přenos popisuje vlastnosti systému v kmitočtové oblasti a je popsán vztahem

,

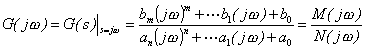(3.1)

kde w je reálný kmitočet [s^-1], tzn. v intervalu (0, ).

Podmínky fyzikální realizovatelnosti:

Kmitočtový přenos G(jw) je funkce komplexní proměnné, takže jej můžeme vyjádřit ve všech základních tvarech:

algebraický tvar:

,

(3.4)

kde je P(w) - reálná část kmitočtového přenosu, Q(w) - imaginární část kmitočtového přenosu, j - imaginární jednotka, ,

exponenciální tvar:

,

(3.5)

A(w) - modul kmitočtového přenosu, , j(w) - fáze kmitočtového přenosu,   .

goniometrický tvar:

,

(3.6)

Kmitočtové charakteristiky jsou grafickým znázorněním kmitočtového přenosu. Pro vykreslování logaritmických kmitočtových charakteristik se rovnice (3.5)  musí zlogaritmovat:

,

(3.7)

Ve skutečnosti se však využívá dekadického logaritmu pro osu úhlového kmitočtu w, tj. log w, a na osu pořadnic amplitudové charakteristiky se vynáší logaritmická amplituda L(w) v decibelech

(3.8)

Kmitočtové charakteristiky v logaritmických souřadnicích se znázorňují dvěmi charakteristikami: logaritmickou amplitudovou kmitočtovou charakteristikou (LAKCH) L(w) a logaritmickou fázovou kmitočtovou charakteristikou (LFKCH)j(w) .

Význam zavedení logaritmických kmitočtových charakteristik (LKCH) spočívá ve zjednodušení výpočtů charakteristik složených systémů a v jejich jednoduchém sestrojování. [Balátě, J. 1996]

Zpět na začátek