Předpokládá se náhradní model asynchronního motoru se synchronně rotujícím prostorovým vektorem statorového proudu v pravoúhlém souřadnicovém systému - (obr. 3.2.). Proto rychlost otáčení souřadnicového systému je rovná synchronní rychlosti asynchronního  motoru.

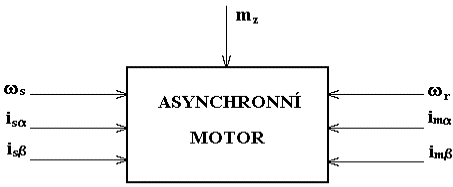
Obr. 3.2 Asynchronní motor – řízený dynamický podsystém

Matematický model

Pro  asynchronní  motor  pak  platí  následující  rovnice :

  napěťové rovnice:

                                                                                       (3.21a)

,                                                                                      (3.21b)

rovnice spřažených magnetických toků:

                                                                                                       (3.22a)

                                                                                                        (3.22b)

rovnice elektromagnetického momentu motoru:

,                                                                                                       (3.23)

pohybová  rovnice  motoru:

                                                                                       (3.24)

      Asynchronní motor je popsán v souřadnicovém systému - soustavou dvou vektorových napěťových rovnic a momentovou rovnicí. Po jejich rozepsání je dynamika asynchronního motoru popsána soustavou pěti rovnic. Podstatného zjednodušení lze dosáhnout zavedením pseudoproudu im definovaného  vztahem :

                                                                                                                   (3.25)

následně  ze  vztahu (3.22) dostaneme:

                                                                                                            (3.26)

Z rovnic (3.21a) a (3.21b) pro ur = 0 po úpravě obdržíme

                                                         (3.27)

a  po uvažování (3.26)

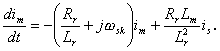                                                                             (3.28)

V souladu s (3.25) a (3.26) vztah na elektromagnetický moment motoru (3.23) bude mít tvar : 

                                                                                         (3.29)

,kde                                              (3.30)

Pohybovou rovnici motoru pak lze zapsat

                                                       (3.31)

Rovnice (3.31) a (3.28)  tvoří matematický model asynchronního motoru. Po rozepsání  vektorové  rovnice  (3.28)  na  složky  dostaneme

                                            (3.32)

                                                                (3.33)

                                                                (3.34)

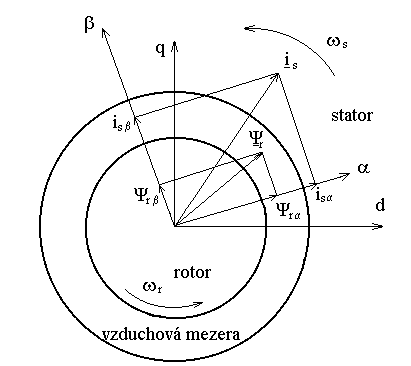
Obr. 3.3 Vektorově orientované řízení

            Cílem vektorově orientovaného řízení asynchronního motoru je, aby prostorový vektor spřaženého magnetického toku rotoru r byl konstantní, aby se otáčel synchronně se souřadnicovým systémem - a aby jeho složka r = 0 , z čehož na základě vztahu (3.25) plyne im  = 0 . Bude-li složka im konstantní, pak ze vztahu (3.29) je zřejmé, že elektromagnetický moment bude úměrný složce statorového proudu is .

            Pro zpětnovazební řízení je nutné znát kromě úhlové rychlosti r také vektor pseudoproudu im. Ze vztahu (3.25) je zřejmé, že je úměrný vektoru spřaženého magnetického toku r, o němž lze získat informaci přímo měřením pomocí měřících cívek nebo Hallových sond, případně nepřímo z měření statorového napětí a proudu.

            Statorové napětí v klidu je dáno vztahem

                                                                                                        (3.35)

            Pokud dosadíme ze vztahu (3.26) do vztahu (3.35) lze vyjádřit vektor spraženého magnetického toku statoru

                                                                                                  (3.36a)

kde                                                                                                  (3.36b)

je činitel rozptylu.

Ze vztahu (3.36) je možno určit vektor pseudoproudu

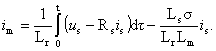                                                                              (3.37)

Na základě matematického modelu (3.32) až (3.34) je zřejmé, že asynchronní motor lze považovat za dynamický podsystém se třemi řídícími veličinami (úhlová rychlost vektoru statorového proudu a složky vektoru statorového proudu ve směrech - ), třemi výstupními veličinami (úhlová rychlost rotoru, složky pseudoproudu ve směrech - ) a jednou poruchovou veličinou (zátěžný moment ), obr 3.2. 

            Zavedením stavových proměnných získáváme stavový model asynchronního motoru.

Zavedení substituce :

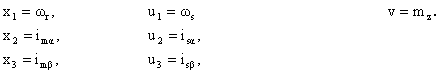                       (3.38)

Stavový model asynchronního motoru :

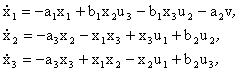                                                                         (3.39)

kde

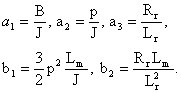                                                                                       (3.40)

resp.

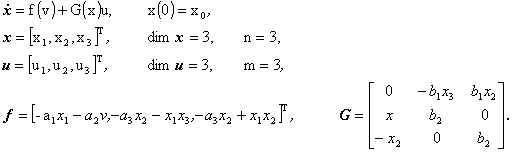    (3.41)

zpět

Návrh nerobustního řízení

Pro nelineární systém na obr. 3.2 navrhuji metodou agregace řízení podle vztahu

Agregační matici navrhujeme s využitím vzorce 1.30.

                                                                       (3.42)

• Určení inverzní matice časových konstant

Transponovaná matice čas. konstant

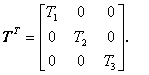                                                                                                (3.43)

Adjungovaná matice T  

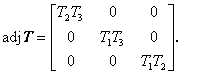                                                                                   (3.44)

Determinant matice T

                                                                                                            (3.45)

Inverzní matice T

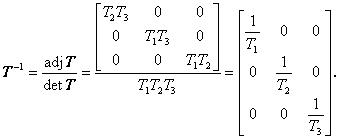                                              (3.46)

• Určení inverzní agregované matice  

Transponovaná matice

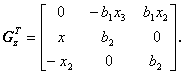                                                                                      (3.47)

Adjungovaná matice G_z

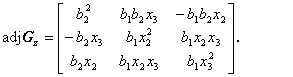                                                           (3.48)

Determinant matice G_z

                                                                                   (3.49)

Inverzní matice G_z

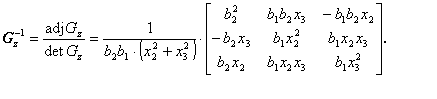                       (3.50) 

Vektor řízení u^* pak má tři složky

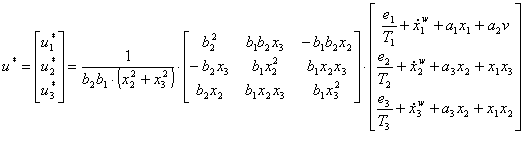(3.51a)

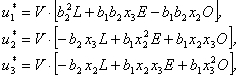                                                                      (3.51b)

kde

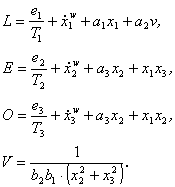                                                                                       (3.51c)

Návrh robustního řízení s vysokým zesílením

V této podkapitole navrhuji robustní řízení založené na metodě agregace stavových proměnných ve tvaru:

.

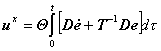Při použití agregační matice a matice časových konstant (3.50)a (3.46), získáváme robustní řízení s vysokým zesílení ve tvaru :

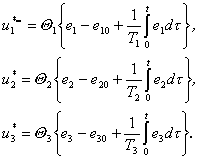                                                                                   (3.52)

zpět

Návrh robustního řízení vycházející z Ljapunovovy funkce

    V této kapitole je je proveden návrh robustního řízení vycházející z Ljapunovovy funkce.

                                                    (3.53)

a)      Využitím funkce sgn(s)

Pro návrh robustního řízení pro nelineární dynamický subsystém na obr. 3.2, získáváme robustní řízení ve tvaru :

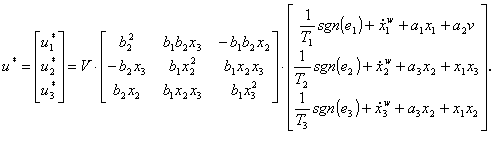       (3.54a)

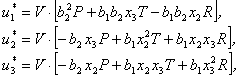                                                                    (3.54b)

kde

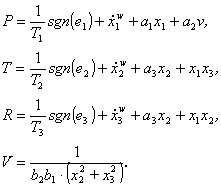                                                                           (3.54c)

b)      Využitím funkce q(s) = sat(Qs)

Pro návrh řízení metodou Ljapunovovy funkce pro nelineární dynamický subsystém na obr. 3.2, reprezentovaný matematickým modelem ve stavovém složkovém zápise (3.4).

 Řízení v obecném tvaru:

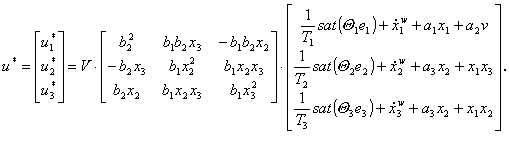   (3.55a)

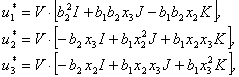                                                                    (3.55b)

kde

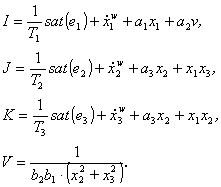                                                                           (3.55c)

c)      Využití funkce q(s) = tgh(Qs)

pro nelineární dynamický subsystém na obr. 3.2, reprezentovaný matematickým modelem ve stavovém složkovém zápise (3.4).

Řízení v obecném tvaru:

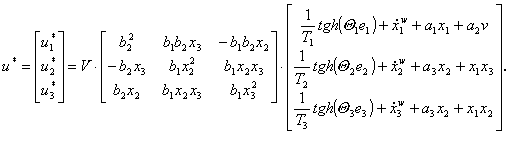   (3.56a)

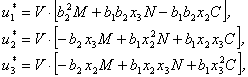                                                                 (3.56b)

kde

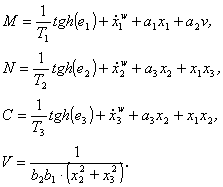                                                                           (3.56c) 

  zpět