Tato podkapitola se podrobně zabývá návrhem programového řízení metodou agregace stavových proměnných na základě účelového funkcionálu.

Programové řízení spočívá v rychlém a přesném sledování předem zadané požadované stavové trajektorie {x^w(t)} skutečnou stavovou trajektorií {x(t)} řízeného nelineárního podsystému, tj. v minimalizaci v každém časovém okamžiku vektoru odchylek.

                         (1.8)

Proto  pro globální hodnocení kvality programového řízení může být  s výhodou použit kvadratický účelový funkcionál

             (1.9)

kde Q, Q₀ jsou symetrické kladně definitní, resp. kladně semidefinitní konstantní váhové matice řádu n.

Je zřejmé, že z důvodu existence funkcionálu (1.9) musí platit

           (1.10)

První výraz v integrandu účelového funkcionálu (1.9) zajišťuje blízkost stavových trajektorií {x(t)} a {x^w(t)}, druhý výraz zajišťuje dostatečnou blízkost i jejich změn v čase, tj. jejich derivací .Vzhledem k tomu, že ke každé časové změně stavu je potřeba určité energie na řízení, tento výraz nepřímo vyjadřuje i spotřebu energie.

Důležitost jednotlivých složek vektorů e a  vyjadřující odpovídající prvky váhových matic Q a Q₀.

Nyní již můžeme zformulovat úlohu optimálního programového řízení:

Pro standardní nelineární podsystém [viz (2.1)]

                                (1.11)

 je třeba určit takové zpětnovazební řízení

                      (1.12),

které minimalizuje kvadratický účelový funkcionál (1.9).

Za předpokladu, že u standardního nelineárního podsystému (1.11) je splněna podmínka řiditelnosti (1.3), resp. (1.7), danou úlohu optimálního programového řízení můžeme řešit poměrně snadno, zavedeme-li vektor agregované odchylky.

           (1.13)

kde D je nezáporná agregační matice [tato agregační matice je obecně jiná než základní agregační matice D_z daná vztahem (1.19)].

Nyní v kvadratickém účelovém funkcionálu (1.14) můžeme vektory e a dimenze n zastoupit odpovídajícími agregovanými vektory s a  dimenze m, tj.

                                                                                               (1.14)

kde

                                                                                   (1.15)

je diagonální matice kladných časových konstant T_j řádu m.

Ze srovnání funkcionálů (1.9) a (1.14) vyplývají rovnosti

                                                                                                  (1.16)

 a dále na základě vztahů (1.10) a (1.13) platí

                                                                                   (1.17)

 Ze vztahů (1.16) je zřejmé, že pro dané matice D a T vždy existují odpovídající váhové matice Q a Q₀, a proto v tomto případě oba funkcionály (1.9) a (1.14) jsou vzájemně ekvivalentní. Pro dané matice Q a Q₀ oba funkcionály budou vzájemně ekvivalentní pouze za předpokladu existence rozkladů (1.16).

Jednoduchá struktura kvadratického účelového funkcionálu  (1.14) umožňuje jeho přímou minimalizací bez použití metod dynamické optimalizace.

Použijme pomocný kvadratický funkcionál

                                                                                               (1.18)

který nabývá svého ostrého globálního minima rovného 0 na časové vektorové funkci , která je řešením lineární diferenciální rovnice

                                                                                             (1.19a)

při počáteční podmínce [viz (2.41)]

                                                                                 (1.19b)

 Řešení diferenciální rovnice (1.19) má jednoduchý tvar

                                                                                   (1.20)

ze kterého  vyplývá přímo interpretace diagonální matice (1.15) jako matice časových konstant.

Ukážeme, že kvadratický účelový funkcionál (1.14) nabývá svého ostrého globálního minima na stejné funkci  jako pomocný kvadratický funkcionál (1.18), tj. na řešení (1.20) diferenciální rovnice (1.19).

Pomocný kvadratický funkcionál (1.18) upravíme

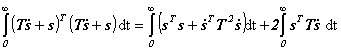                                               (1.21)

a poslední výraz integrujeme metodou per partes s využitím koncových podmínek (1.17):

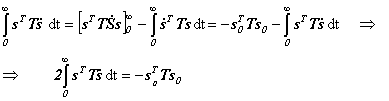                                   (1.22)

 Na základě vztahů (1.21) a (1.22) dostaneme velmi důležitou rovnost

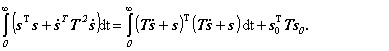                                   (1.23)

 Protože hodnota [viz (1.19b)]

                                   (1.24)

 je konstantní, z rovnosti (1.23) vyplývá, že kvadratický účelový funkcionál (1.14) nabývá svého ostrého globálního minima rovného hodnotě (1.24) na stejné funkci  jako pomocný kvadratický funkcionál (1.18).

Je rovněž zřejmé, že pokud platí vztahy (1.16), je hodnota (1.24) současně i ostrým globálním minimem původního kvadratického účelového funkcionálu (1.9).

Diferenciální rovnice (1.19) popisuje vlastnosti optimálního uzavřeného systému řízení vzhledem k vektoru agregované odchylky s. Po dosazení (1.13) do (1.19) a úpravě obdržíme agregovanou diferenciální rovnici optimálního uzavřeného systému řízení vyjádřenou vzhledem k vektoru odchylek e, tj.

                                                           (1.25)

kde v souladu s (1.8) a (1.11)

                                                                                 (1.26)

Ve vztazích (1.25) a (1.26) z důvodu větší přehlednosti nejsou hvězdičkami * označeny vektory e,  a x podobně jako vektory s a v rovnici (1.19a), i když jsou optimální.

Bude-li platit

                                                                                                 (1.27)

pak ze vztahů (1.25) a (1.26) můžeme již snadno určit optimální zpětnovazební řízení

                                               (1.28)

Ze vztahu (1.28) je zřejmé, že kromě zadané stavové trajektorie {x^w(t)} musíme rovněž znát i její derivaci { ^w(t)}.

Pokud budeme uvažovat ^w(t)=0 (stabilizační řízení), pak úloha optimálního řízení spočívá v převedení daného nelineárního podsystému (1.11) z počátečního stavu x(0)= x₀ do zadaného koncového stavu  a setrvání v něm při minimální hodnotě kvadratického účelového funkcionálu (1.9). I v tomto případě minimální hodnota funkcionálu (1.9) je dána vztahem (1.24).

Optimální uzavřený systém řízení (1.25) můžeme vyjádřit v obvyklém tvaru (při uvažovaní rovnic )

                                                                                   (1.29)

kde A je stavová matice dynamiky uzavřeného systému řízení řádu n.

Zvolíme-li prvky d_ji agregační matice D v souladu se vztahem [viz(2.1a)]

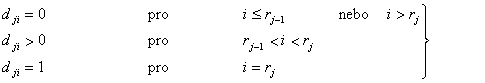           (1.30)

pak charakteristický mnohočlen optimálního uzavřeného systému řízení (1.29), resp. (1.25) bude

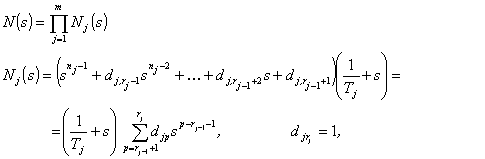      (1.31a,b)

kde s je komplexní proměnná v Laplaceově transformaci, - charakteristický mnohočlen j-tého autonomního podsystému řízení řádu n_j.

Je tedy zřejmé, že v tomto případě optimální uzavřený systém řízení (1.25), resp. (1.29) je tvořen m  autonomními lineárními podsystémy řízení, jejichž požadované  dynamické vlastnosti můžeme snadno zajistit vhodnou volbou časových konstant T_j a koeficientů d_ji jejich charakteristických mnohočlenů (1.31b), tj. vhodnou volbou matic T a D. Je to nesmírně důležité, protože požadované dynamické vlastnosti uzavřeného systému řízení (1.25), resp. (1.29), tj. požadovanou kvalitu programového řízení vyjádřenou minimální hodnotou kvadratického účelového funkcionálu (1.9) zaručíme bez nutnosti předchozí znalosti váhových matic Q a Q₀. Vidíme tedy, že kvadratický účelový funkcionál (1.9) má pouze pomocnou roli a že při jeho minimalizaci došlo ke zpětnovazební linearizaci typu „vstup – stav“. Tato linearizace spočívá v kompenzaci všech nelinearit včetně poruch a dodání takových lineárních výrazů, které zajistí požadované lineární vlastnosti uzavřeného systému řízení. Je zřejmé, že v případě nedostatečné znalosti matematického modelu řízeného nelineárního podsystému, resp. neměřitelnosti poruch, může dojít k nedokonalé kompenzaci a uzavřený systém řízení nemusí dosáhnout požadované kvality řízení a může být dokonce nestabilní.

Zvolíme-li agregační matici D v souladu se vztahy (1.30), což budeme vždy předpokládat, pak platí [viz (1.4) a (1.5)]

                                                           (1.32)

 a optimální zpětnovazební řízení (1.28) můžeme zapsat také ve tvaru

                                                           (1.33)

Protože zpětnovazební algoritmus řízení (1.28), resp. (1.33) vyžaduje znalost přesného matematického modelu řízeného nelineárního podsystému (1.11) včetně plné měřitelnosti poruch v, je zřejmé, že tento algoritmus nedovede reagovat na nepřesnosti a změny ve vlastnostech řízeného nelineárního podsystému ani na neměřitelné poruchy, a proto je to nerobustní algoritmus řízení.

V této podkapitole je ukázáno, že vhodnou agregací stavových proměnných standardního nelineárního podsystému lze jejich počet snížit na počet řídicích proměnných, který většinou bývá podstatně nižší. Dojde tak ke zjednodušení návrhu programového řízení. Při návrhu řízení na základě účelového funkcionálu dochází ke zpětnovazební linearizaci, a proto uzavřený systém řízení je lineární. Umožňuje to jednoduše zajistit požadované vlastnosti uzavřeného systému řízení pomocí vhodné volby agregační matice D a diagonální matice časových konstant T bez nutnosti řešení optimalizační úlohy, tj. bez nutnosti minimalizace výchozího účelového funkcionálu. Uvedený přístup je velmi jednoduchý, inženýrský, a v případě standardních nelineárních podsystému (tj. bez nutné transformace na standardní tvary) může být použit přímo bez hlubokých teoretických znalostí jak nelineárního, tak i optimálního řízení.