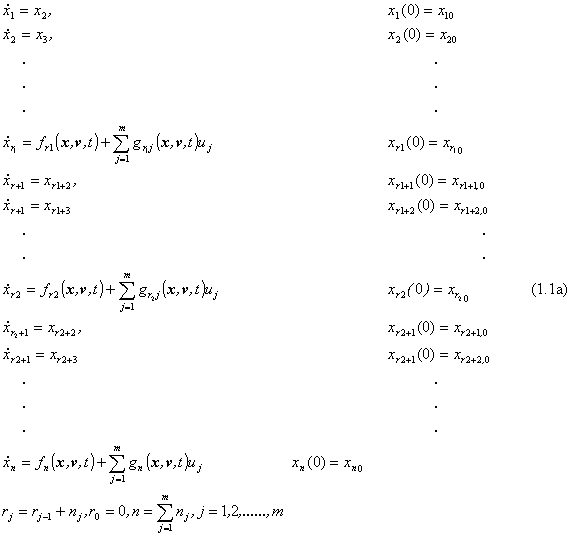
V této kapitole jsou uvedeny původní přístupy k návrhu programového řízení nelineárních podsystémů využívající metodu agregace stavových proměnných [Víteček 1991]. Metoda agregace spočívá ve vhodné volbě agregovaných proměnných, které sníží počet původních stavových proměnných, a tím sníží i dimenzi vlastního problému řízení, což podstatným způsobem zjednoduší jeho řešení.
Uvažujme poměrně obecný řízený nelineární dynamický podsystém, jehož matematický model má ve složkovém vyjádření tvar:
![]()
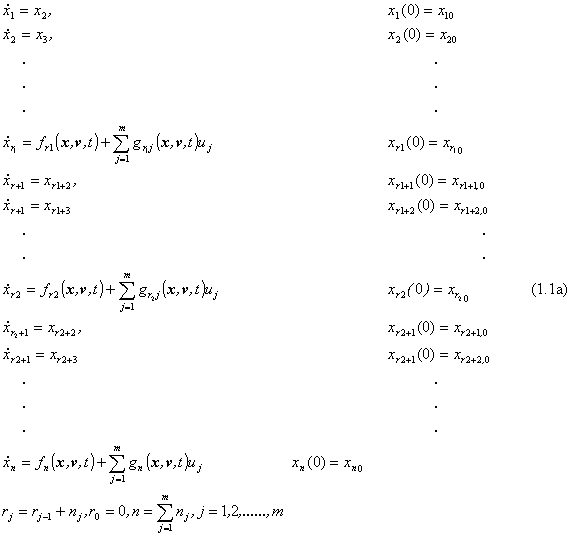
Kompaktněji a přehledněji lze matematický model (1.1a) zapsat vektorově ve tvaru
![]() (1.1b)
(1.1b)
resp.
![]() (1.1c)
(1.1c)
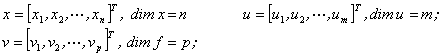
![]()
![]()
kde:
x - vektor stavových proměnných dimenze, n
xo - vektor počátečních hodnot stavových proměnných dimenze n,
u -
vektor řídicích proměnných dimenze m,
v - vektor měřitelných poruchových proměnných dimenze p,
f a Df
– spojité vektorové funkce dimenze n,
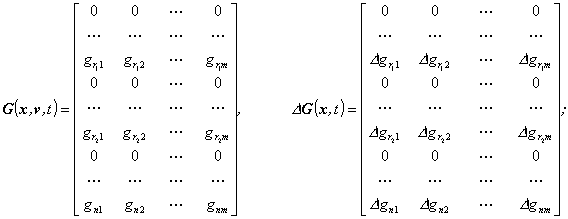
G a DG – matice spojitých funkcí gij a Dgij typu (n, m),
n - je počet stavových proměnných (řád nelineárního podsystému),
nj – dílčí řád.
Výrazy Df a DG mohou vyjadřovat např. neurčitost v chování nelineárního podsystému, nepřesnost identifikace, vliv neměřitelných poruch aj. Mají nulové složky, resp. řádky, které odpovídají nulovým řádkům v matici G.
Je zřejmé, že nelineární podsystém (1.1) lze psát ve tvaru
![]() (1.2)
(1.2)
je považován za nominální tvar.
Podsystém je řiditelný,
existuje –li takové řízení u, které ho převede z libovolného
počátečního stavu x(t0) do libovolného koncového
stavu x(t1) za konečnou dobu t1 – t0.
Pro standardní nelineární podsystémy podmínka říditelnosti má velmi jednoduchý tvar
![]() (1.3)
(1.3)
kde rank znamená hodnost matice. Následně agregovanou matici lze vypočítat ze vztahu
![]() (1.4)
(1.4)
matice Dz – základní nezáporná agregační matice typu (m,n), jejíž prvky jsou dány vztahy
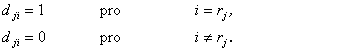 (1.5)
(1.5)
Je-li splněna podmínka (1.5), platí
![]() (1.6)
(1.6)
Vztah (1.6) dovoluje zastoupit podmínku (1.3) jednodušší ekvivalentní podmínkou
![]() (1.7)
(1.7)